
Różnica między wynikiem Z a wynikiem T.
Wynik Z jest konwersją surowych danych do wyniku standardowego, gdy konwersja jest oparta na średniej populacji i standardowym odchyleniu populacji. Gdy dostępny jest u nas pełny zestaw danych, możemy obliczyć wynik Z. Wynik Z jest odejmowaniem średniej populacji od wyniku surowego, a następnie dzieli wynik z odchyleniem standardowym populacji. Wynik T jest konwersją surowych danych do wyniku standardowego, gdy konwersja jest oparta na średniej próbki i odchyleniu standardowym próbki. Gdy zestaw danych populacji nie jest dostępny, musimy pobrać niektóre dane próbki, aby obliczyć średnią próbki i odchylenie standardowe populacji.
Wynik Z.
W normalnym rozkładzie, w którym dostępne są pełne dane, jest to odległość od średniej. Jego formuła jest podana poniżej,
Z= (x-μ)/σ
Gdzie,
X = pojedyncze surowe dane
μ = średnia populacji
σ = standardowe odchylenie populacji
Wynik T.
Wynik T to odjęcie indywidualnego odchylenia standardowego od indywidualnej średniej, a następnie podzielenie wyniku przez cały wynik odchylenia standardowego próbki pomnożony przez wielkość próbki. Jego formuła jest podana poniżej,
t = ((- μ)/s)*
= średnia próbki
μ = średnia populacji
s = przykładowe odchylenie standardowe
n = wielkość próbki
Weźmy przykład, aby zrozumieć to samo w lepszy sposób:
W artykule są 3 podrejony - I, II i III. Niech liczba uczniów, którzy odpowiedzieli poprawnie, będzie wynosić 25%, tj. 75% nie będzie w stanie poprawnie odpowiedzieć na to pytanie. Podobnie, niech 10% i 20% liczby osób, które poprawnie odpowiedziały na sekcje II i III, a zatem 90% i 80% znalazło sekcje II i III. Zakładamy, że zdolność mierzona tymi trzema przedmiotami jest taka sama i zwykle jest dystrybuowana,
Wynik dla każdego ucznia w klasie służy do obliczenia średniej ocen, która jest równa 50 i odchyleniu standardowemu 10. Możemy obliczyć wynik Z z wynikiem 50 jako (50-50) / 10 = 0
Możemy zinterpretować, że wynik studenta wynosi 0 odległości (w jednostkach odchyleń standardowych) od średniej, więc uczeń uzyskał średnią.
Jeśli wynik wynosi 60, wynik Z wynosi (60-50) / 10 = 1
Możemy zinterpretować, że uczeń uzyskał wynik powyżej średniej - odległość 1 odchylenia standardowego powyżej średniej.
Bezpośrednie porównanie między wynikiem Z a wynikiem T (infografiki)
Poniżej znajduje się 9 najważniejszych różnic między wynikiem Z a wynikiem T. 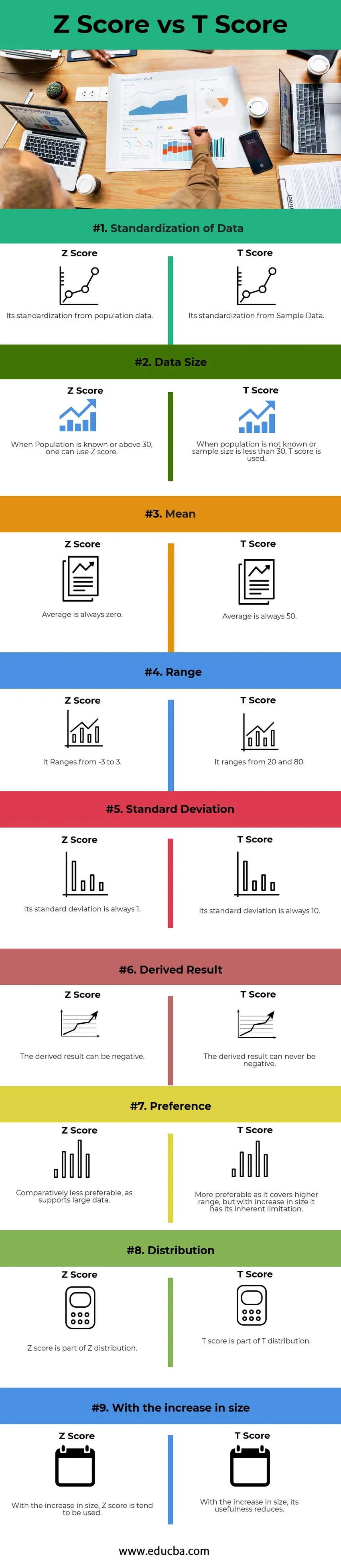
Kluczowe różnice między wynikiem Z a wynikiem T.
Omówmy niektóre z głównych różnic między wynikiem Z a wynikiem T.
- Wynik Z to standaryzacja od surowych danych populacji lub ponad 30 danych próbki do wyniku standardowego, podczas gdy wynik T to standaryzacja od danych próbki mniejszych niż 30 danych do wyniku standardowego
- Wynik Z waha się od -3 do 3, podczas gdy wynik T waha się od 20 do 80.
- Wraz ze wzrostem wielkości danych rozkład ma tendencję do rozkładu Z. Oba wyniki Z w porównaniu z rozkładem T są częścią rozkładu normalnego, ale na podstawie wielkości różnią się od siebie
- Praktycznie wynik Z jest szeroko stosowany w danych giełdowych i do sprawdzania prawdopodobieństwa bankructwa firmy, podczas gdy wynik t jest szeroko stosowany do sprawdzania gęstości mineralnej kości i oceny ryzyka złamania
Wynik Z w porównaniu z wynikiem T
Spójrzmy na 9 najlepszych porównań między wynikiem Z a wynikiem T.
| Sr. No. | Punkty porównania | Wynik Z. | Wynik T. |
| 1 | Standaryzacja danych | Jego standaryzacja na podstawie danych o populacji | Jego standaryzacja na podstawie danych próbek |
| 2) | Rozmiar danych | Kiedy populacja jest znana lub przekracza 30, można użyć wyniku Z. | Gdy populacja nie jest znana lub wielkość próby jest mniejsza niż 30, stosuje się wynik T. |
| 3) | Oznaczać | Średnia to zawsze zero. | Średnia to zawsze 50. |
| 4 | Zasięg | Wynosi od -3 do 3. | Wynosi od 20 do 80. |
| 5 | Odchylenie standardowe | Standardowe odchylenie wynosi zawsze 1 | Standardowe odchylenie wynosi zawsze 10 |
| 6 | Wynik pochodny | Wynik pochodny może być ujemny | Wynik uzyskany nigdy nie może być ujemny |
| 7 | Pierwszeństwo | Stosunkowo mniej preferowany, ponieważ obsługuje duże dane | Bardziej korzystne, ponieważ obejmuje większy zakres, ale wraz ze wzrostem wielkości ma swoje nieodłączne ograniczenia |
| 8 | Dystrybucja | Wynik Z jest częścią rozkładu Z. | Wynik T jest częścią rozkładu T. |
| 9 | Wraz ze wzrostem wielkości | Wraz ze wzrostem wielkości zwykle stosuje się wynik Z. | Wraz ze wzrostem wielkości zmniejsza się jego przydatność. |
Wniosek
Zarówno wynik Z w porównaniu do wyniku T jest częścią testu hipotez w normalnym rozkładzie. Jeśli masz zestaw wyników pomiarów dla różnych miar przy użyciu wyników Z, możesz powiedzieć, w jaki sposób wyniki są umieszczane w ich rozkładach. Następnie możesz je porównać. Standaryzacja wyników jest szeroko stosowaną procedurą w dziedzinie badań i planowania, ponieważ pomaga w porównywaniu różnych wyników testów. Standaryzacja wyników przed ich połączeniem pomaga badaczowi uzyskać lepsze i porównywalne wyniki.
Polecane artykuły
To był przewodnik po najwyższej różnicy między wynikiem Z a wynikiem T. Tutaj omawiamy również kluczowe różnice wyniku Z w porównaniu z wynikiem T z infografiką i tabelą porównawczą. Możesz także zapoznać się z następującymi artykułami, aby dowiedzieć się więcej-
- Finanse a ekonomia - największa różnica
- Deficyt kontra dług - który z nich jest lepszy
- Zakup aktywów a zakup akcji
- Rynek pieniężny a rynek kapitałowy
- Przegląd wyniku Altman Z.