
Średnia arytmetyczna (spis treści)
- Formuła
- Przykłady
- Kalkulator
Co to jest średnia arytmetyczna?
Termin „średnia arytmetyczna” zasadniczo odnosi się do średniej matematycznej dwóch lub więcej liczb. Jednak metoda obliczania średniej arytmetycznej może się różnić w zależności od częstotliwości każdej zmiennej w zbiorze danych - zwykła średnia (równo ważona) lub średnia ważona. Wzór na średnią arytmetyczną dla równo ważonych zmiennych można uzyskać, sumując wszystkie zmienne w zbiorze danych, a następnie dzieląc wynik przez liczbę zmiennych. Matematycznie jest reprezentowany jako
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
lub
Arithmetic Mean =∑ x i / n
Gdzie,
- x i = i- ta zmienna
- n = liczba zmiennych w zbiorze danych
W przypadku nierównomiernie ważonych zmiennych wzór na średnią arytmetyczną można uzyskać, sumując iloczyn każdej zmiennej i jej częstotliwość, a następnie wynik dzieli się przez sumę częstotliwości. Matematycznie jest reprezentowany jako
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
lub
Arithmetic Mean = ∑ (f i * x i ) / f i
Gdzie
- x i = i- ta zmienna
- f i = Częstotliwość i- tej zmiennej
Przykłady średniej arytmetycznej formuły (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie średniej arytmetycznej.
Możesz pobrać ten szablon Excel ze średnią arytmetyczną tutaj - szablon Excel ze średnią arytmetycznąWzór średniej arytmetycznej - przykład nr 1
Weźmy przykład pałkarza, który w ostatnich 10 rundach strzelił następujące biegi: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Oblicz średnią pałkarza w jego ostatnich 10 inningów.
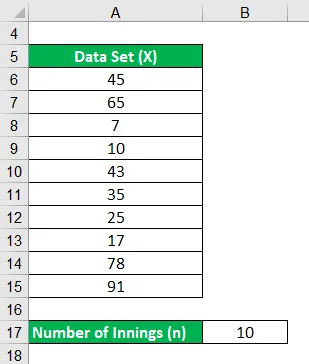
Rozwiązanie:
Średnia arytmetyczna jest obliczana przy użyciu poniższego wzoru
Średnia arytmetyczna = ∑ x i / n
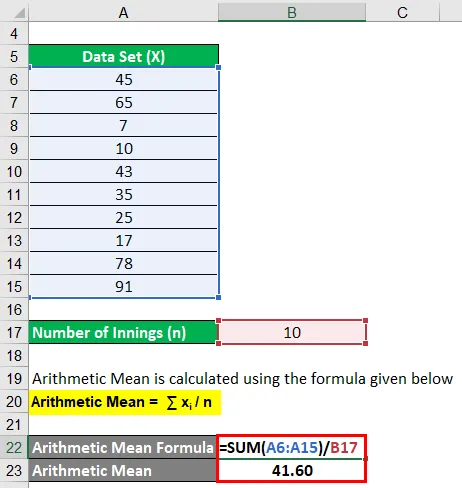
- Średnia arytmetyczna = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Średnia arytmetyczna = 41, 60
Dlatego średnia pałkarza wynosiła 41, 60 przebiegów na rundy w jego ostatnich 10 rundach.
Wzór średniej arytmetycznej - przykład nr 2
Weźmy przykład klasy z 45 uczniami. Niedawno przeprowadzono cotygodniowy test naukowy, w którym uczniowie byli oceniani w skali od 1 do 10. Na podstawie poniższych informacji obliczyć średnie oceny z testu.
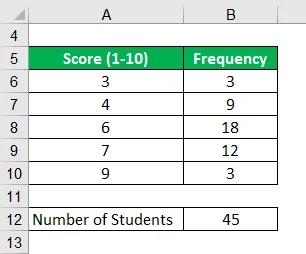
Rozwiązanie:
Średnia arytmetyczna jest obliczana przy użyciu poniższego wzoru
Średnia arytmetyczna = ∑ (f i * x i ) / f i
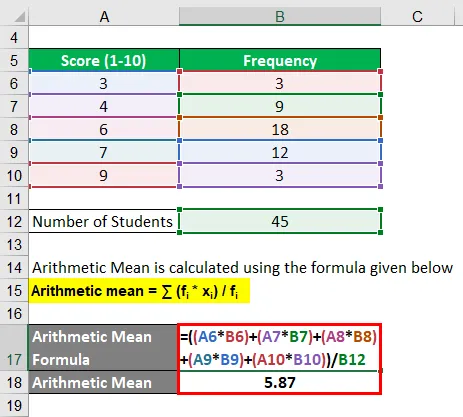
- Średnia arytmetyczna = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Średnia arytmetyczna = 264/45
- Średnia arytmetyczna = 5, 87
Dlatego średni wynik klasy w teście naukowym wynosił 5, 87.
Wzór średniej arytmetycznej - przykład nr 3
Weźmy przykład dwóch zestawów danych z dwoma różnymi średnimi arytmetycznymi. Pierwszy zestaw danych ma 10 zmiennych ze średnią 45, podczas gdy drugi zestaw danych ma 7 zmiennych i średnią 42. Określić średnią arytmetyczną dwóch połączonych zestawów danych.
Rozwiązanie:
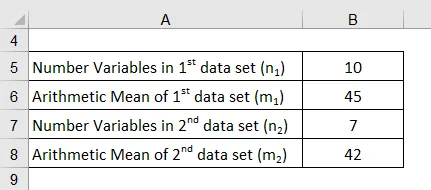
Średnie arytmetyczne połączonego zestawu danych oblicza się przy użyciu poniższego wzoru
Średnia arytmetyczna = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
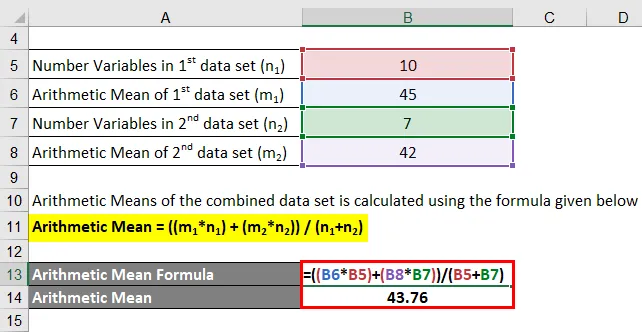
- Średnia arytmetyczna = (45 * 10 + 42 * 7) / (10 + 7)
- Średnia arytmetyczna = 43, 76
Dlatego średnie arytmetyczne połączonego zestawu danych wynoszą 43, 76.
Wyjaśnienie
Wzór na średnią arytmetyczną można obliczyć, wykonując następujące czynności:
Krok 1: Po pierwsze, zbierz i uporządkuj zmienne, dla których należy obliczyć średnią arytmetyczną. Zmienne są oznaczone x i .
Krok 2: Następnie określ liczbę zmiennych w zbiorze danych i jest oznaczona przez n w przypadku zmiennych o równej wadze. W przeciwnym razie obliczyć częstotliwość każdej zmiennej i są one oznaczone przez fi, a liczba zmiennych jest sumą częstotliwości.
Krok 3: Wreszcie wzór na średnią arytmetyczną dla zmiennych o równej wadze można uzyskać, dodając wszystkie zmienne, a następnie wynik dzieli się przez liczbę zmiennych w zestawie danych, jak pokazano poniżej.
Średnia arytmetyczna = ∑ x i / n
Jednak w przypadku średniej ważonej wzór na średnią arytmetyczną można uzyskać przez zsumowanie iloczynu każdej zmiennej i jej częstotliwości, a następnie wynik dzieli się przez sumę częstotliwości, jak pokazano poniżej.
Średnia arytmetyczna = ∑ f i * x i / f i
Trafność i zastosowania średniej arytmetycznej
Pojęcie średniej arytmetycznej jest bardzo proste i elementarne. Jest to jednak nadal bardzo ważne, ponieważ jest często wykorzystywane jako wskaźnik statystyczny do oceny średniego wyniku w zbiorze danych. W rzeczywistości pozwala ocenić, które ze zmiennych są lepsze lub niższe niż średnia w grupie. Służy również jako miara reprezentująca średnią wartość dla całej serii danych. Ponadto średnią arytmetyczną stosuje się w przypadkach, gdy średnia geometryczna lub średnia harmoniczna są mniej przydatne, takie jak średnia ocena, waga itp.
Kalkulator średniej arytmetycznej
Możesz użyć następującego kalkulatora średniej arytmetycznej
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Średnia arytmetyczna | |
| Średnia arytmetyczna | = |
|
|
Polecane artykuły
Jest to przewodnik po średniej arytmetycznej. Tutaj omawiamy, jak obliczyć średnią arytmetyczną wraz z praktycznymi przykładami. Oferujemy również kalkulator średniej arytmetycznej z szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Jak obliczyć średnią harmoniczną?
- Przewodnik po średniej liczby mieszkańców
- Obliczanie średniej za pomocą Formula
- Przykłady formuły sprzedaży netto