
Wzór na efektywną stopę procentową (spis treści)
- Formuła
- Przykłady
- Kalkulator
Jaka jest formuła efektywnej stopy procentowej?
Termin „efektywna stopa procentowa” odnosi się do prawdziwej rocznej rentowności inwestycji, która jest uzyskiwana w wyniku powiększania się w czasie. I odwrotnie, efektywną stopę procentową można postrzegać jako prawdziwy koszt pożyczki z punktu widzenia pożyczkobiorcy. Jest również znany jako efektywny roczny zwrot lub roczna stopa równoważna. Wzór na efektywną stopę procentową można wyprowadzić na podstawie podanej stopy procentowej i liczby okresów łączenia w ciągu roku. Matematycznie jest reprezentowany jako
Effective Interest Rate = (1 + i/n) n – 1
gdzie,
- i = Podana stopa procentowa
- n = liczba złożonych okresów rocznie
Przykłady formuły efektywnej stopy procentowej (z szablonem Excel)
Weźmy przykład, aby lepiej obliczyć efektywną stopę procentową.
Możesz pobrać ten szablon Excel z formułą efektywnej stopy procentowej - Szablon Excel z efektywną stopą procentowąWzór na efektywną stopę procentową - przykład nr 1
Weźmy przykład inwestycji o podanej stopie procentowej wynoszącej 10%. Oblicz efektywną stopę procentową, jeśli inwestycja ma być powiększana dwa razy w roku.
Rozwiązanie:
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1

- Efektywna stopa procentowa = (1 + 10% / 2) 2 - 1
- Efektywna stopa procentowa = 10, 25%
Dlatego efektywna stopa procentowa dla notowanej inwestycji wynosi 10, 25%.
Wzór na efektywną stopę procentową - przykład nr 2
Weźmy przykład Johna, który jest zainteresowany inwestowaniem obligacji, która oferuje określoną stopę procentową w wysokości 9%. Jednak natura łączenia jest inna i John nie jest pewien, które połączenie przyniesie najwyższy zwrot. Oblicz efektywną stopę procentową i pomóż Johnowi podjąć owocną decyzję w następującym okresie mieszania:
- Roczny
- Półroczne
- Kwartalny
- Miesięczny
- Codziennie
Roczny
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1
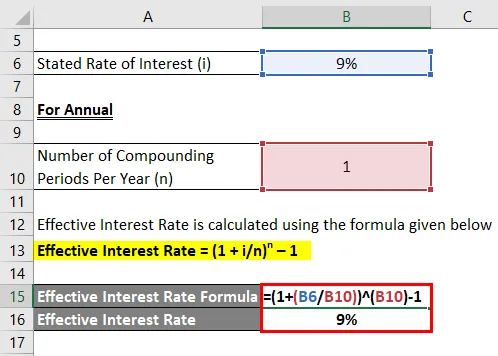
- Efektywna stopa procentowa = (1 + 9% / 1) 1 - 1
- Efektywna stopa procentowa = 9%
Półroczne
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1
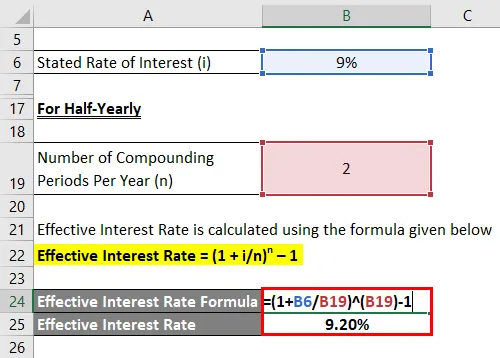
- Efektywna stopa procentowa = (1 + 9% / 2) 2 - 1
- Efektywna stopa procentowa = 9, 20%
Kwartalny
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1
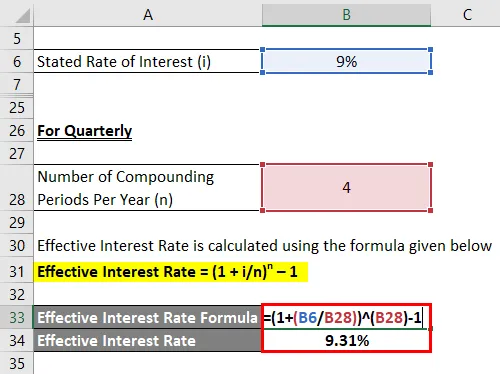
- Efektywna stopa procentowa = (1 + 9% / 4) 4 - 1
- Efektywna stopa procentowa = 9, 31%
Miesięczny
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1
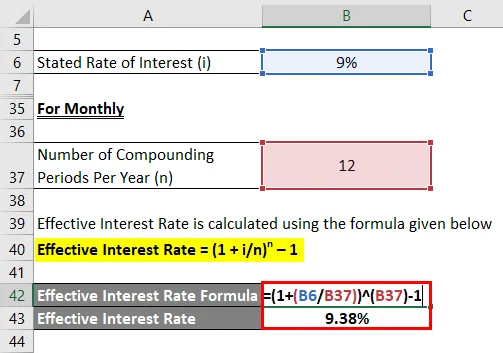
- Efektywna stopa procentowa = (1 + 9% / 12) 12 - 1
- Efektywna stopa procentowa = 9, 38%
Codziennie
Efektywna stopa procentowa jest obliczana przy użyciu poniższego wzoru
Efektywna stopa procentowa = (1 + i / n) n - 1

- Efektywna stopa procentowa = (1 + 9% / 365) 365-1
- Efektywna stopa procentowa = 9, 42%
Dlatego wyraźnie widać, że roczna wydajność rośnie wraz ze wzrostem liczby mieszań w ciągu roku. Jako taka, opcja codziennego mieszania zapewni najlepszą rentowność dla Johna (efektywne oprocentowanie w wysokości 9, 38% w stosunku do podanej stopy oprocentowania wynoszącej 9%).
Wyjaśnienie
Wzór na efektywną stopę procentową można uzyskać, wykonując następujące czynności:
Krok 1: Po pierwsze, ustal deklarowane oprocentowanie inwestycji, które zwykle jest wymienione w dokumencie inwestycyjnym. Jest oznaczony przez „i”.
Krok 2: Następnie obliczyć liczbę okresów złożonych w ciągu roku i jest to oznaczone jako „n”. Zwykle mieszanie odbywa się co kwartał, co pół roku i co rok, co oznacza liczbę związków odpowiednio 4, 2 i 1 rocznie.
Krok 3: Wreszcie wzór na efektywną stopę procentową można uzyskać, stosując podaną stopę procentową (krok 1) i liczbę okresów łączenia w ciągu roku (krok 2), jak pokazano poniżej.
Efektywna stopa procentowa = (1 + i / n) n - 1
Trafność i zastosowania formuły efektywnej stopy procentowej
Ważne jest zrozumienie koncepcji efektywnej stopy procentowej, ponieważ jest to niezbędny wskaźnik dla inwestora lub innego użytkownika finansowego. Inwestorzy zwykle stosują efektywną stopę procentową, ponieważ jest to faktyczny zysk uzyskany z inwestycji. W związku z tym inwestorzy kładą większy nacisk na liczbę mieszań rocznie, ponieważ większa liczba mieszań oznacza większą wydajność. Z drugiej strony zmienia się perspektywa dla pożyczkobiorcy, który dąży do zmniejszenia liczby składek rocznie, ponieważ utrzyma to niskie koszty odsetek i poprawi rentowność.
Koncepcja efektywnej stopy procentowej jest bardzo zależna od liczby zjawisk składających się w ciągu roku, które ostatecznie dają wyższą rentowność lub ostatecznie wyższą wartość wykupu w terminie zapadalności. Zazwyczaj efektywna stawka roczna rośnie wraz ze wzrostem liczby składników rocznie. Chociaż mieszanie można wykonać nieskończoną liczbę razy, należy pamiętać, że istnieje pewien limit efektu mieszania i po przekroczeniu którego zjawisko przestaje występować. Ten rodzaj mieszania jest znany jako ciągłe mieszanie, dla którego efektywna stopa procentowa jest wyrażona jako - e i, i jest podaną stopą procentową i jest niezależna od okresu mieszania.
Kalkulator efektywnej formuły stopy procentowej
Możesz użyć następującego kalkulatora efektywnej stopy procentowej
| ja | |
| n | |
| Efektywna stopa procentowa | |
| Efektywna stopa procentowa = | (1 + i / n) n -1 |
| = | (1 + 0/0) 0 -1 = 0 |
Polecane artykuły
Jest to przewodnik po formule efektywnej stopy procentowej. Tutaj omawiamy sposób obliczania efektywnej stopy procentowej wraz z praktycznymi przykładami. Oferujemy również kalkulator efektywnej stopy procentowej z szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Wzór na miesięczne odsetki złożone
- Jak obliczyć nominalną stopę procentową?
- Przykłady kosztów odsetek
- Obliczanie formuły nominalnego PKB
- Odsetki vs dywidenda | 8 najważniejszych różnic, które powinieneś znać