
Formuła testu F (spis treści)
- Formuła
- Przykłady
Co to jest formuła testu F?
Test F jest testem statystycznym, który pomaga nam ustalić, czy dwa zestawy populacji, które mają normalny rozkład ich punktów danych, mają to samo odchylenie standardowe lub wariancje. Ale pierwszą i najważniejszą rzeczą do wykonania testu F jest to, że zbiory danych powinny mieć rozkład normalny. Odnosi się to do rozkładu F w ramach hipotezy zerowej. Test F jest bardzo istotną częścią Analizy wariancji (ANOVA) i jest obliczany na podstawie stosunków dwóch wariancji dwóch różnych zestawów danych. Jak wiemy, wariancje dostarczają nam informacji o rozproszeniu punktów danych. Test F jest również stosowany w różnych testach, takich jak analiza regresji, test Chow itp.
Wzór na test F:
Nie ma prostej formuły testu F, ale jest to szereg kroków, które musimy wykonać:
Krok 1: Aby wykonać test F, najpierw musimy zdefiniować hipotezę zerową i hipotezę alternatywną. Są one podawane przez:
- H0 (hipoteza zerowa): wariancja 1. zestawu danych = wariancja 2. zestawu danych
- Ha: Odchylenie pierwszego zestawu danych <Odchylenie drugiego zestawu danych (dla niższego jednostronnego testu)
- Ha: Odchylenie pierwszego zestawu danych> Odchylenie drugiego zestawu danych (dla górnego testu jednostronnego)
- Ha: Odchylenie pierwszego zestawu danych ≠ Odchylenie drugiego zestawu danych (dla testu dwustronnego)
Krok 2: Następnie musimy ustalić poziom istotności, a następnie określić stopnie swobody zarówno licznika, jak i mianownika. Pomaga nam to określić ich wartości krytyczne. Stopień swobody to wielkość próbki -1.
Krok 3: Formuła testu F:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Krok 4: Znajdź wartość krytyczną F z tabeli F biorąc stopień swobody i poziom znaczenia.
Krok 5: Porównaj te dwie wartości, a jeśli wartość krytyczna jest mniejsza niż wartość F, możesz odrzucić hipotezę zerową.
Przykłady formuły F-Test (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczenia testu F.
Możesz pobrać ten szablon Excel Formula F-TEST tutaj - Szablon Excel Formula F-TESTFormuła testu F - przykład nr 1
Załóżmy, że mamy dwa zestawy danych A i B, które zawierają różne punkty danych. Wykonaj test F, aby ustalić, czy możemy odrzucić hipotezę zerową przy poziomie istotności 1%.
Zestawy danych:
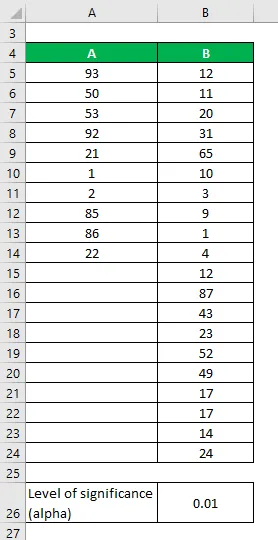
Rozwiązanie:
Hipoteza zerowa: wariancja A = wariancja B
Stopień swobody oblicza się jako
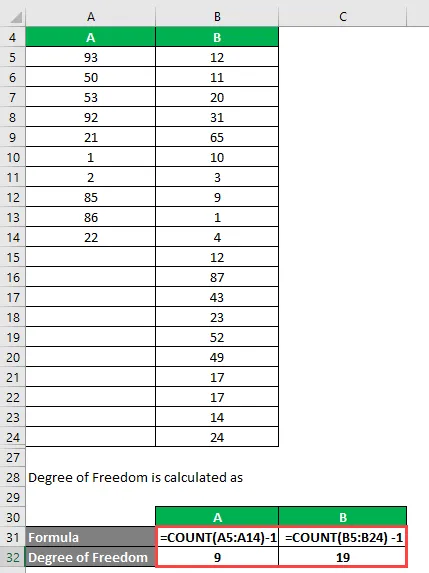
Stopień wolności
- Dla A = 10-1 = 9
- Dla B = 20-1 = 19
Zmienność jest obliczana jako:

- Wariancja A = 1385, 61
- Wariancja B = 521, 22
Wartość F oblicza się przy użyciu poniższego wzoru
Wartość F = wariancja 1. zestawu danych / wariancja 2. zestawu danych
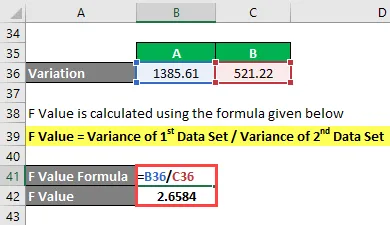
- Wartość F = 1385, 61 / 521, 22
- Wartość F = 2, 6584
Tabela F:
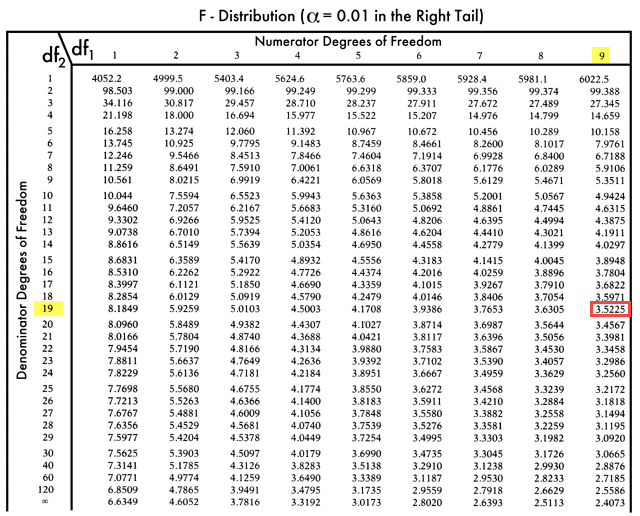
Zatem wartość krytyczna F = 3, 5225
Ponieważ krytyczna wartość F jest większa niż wartość F, nie możemy odrzucić hipotezy zerowej.
Formuła testu F - Przykład 2
Załóżmy, że pracujesz w firmie badawczej i chcesz, aby poziom emisji tlenku węgla pochodził z 2 różnych marek papierosów i czy były one znacząco różne, czy nie. W swojej analizie zgromadziłeś następujące informacje:
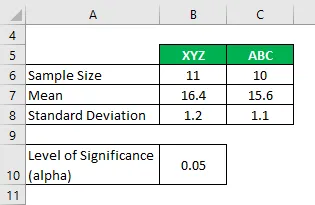
Rozwiązanie:
Stopień swobody oblicza się jako
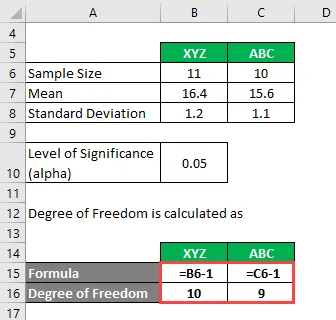
Stopień wolności
- Dla XYZ = 11-1 = 10
- Dla ABC = 10-1 = 9
Zmienność jest obliczana jako:
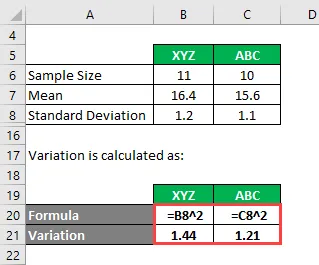
- Wariancja XYZ = 1, 2 2 = 1, 44
- Wariancja ABC = 1, 1 2 = 1, 21
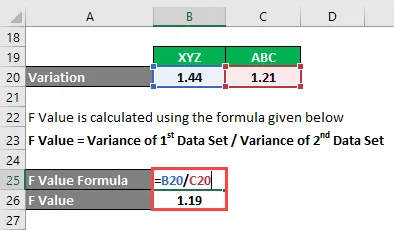
- Wartość F = 1, 44 / 1, 21
- Wartość F = 1, 19
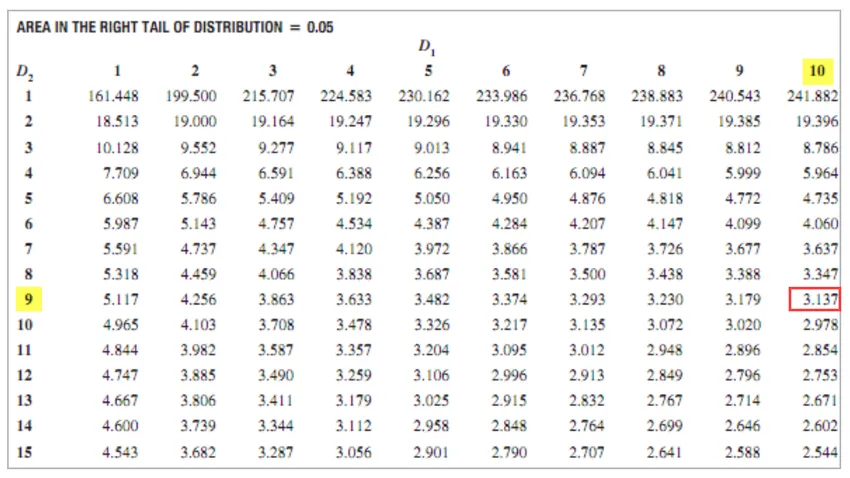
F Wartość krytyczna = 3, 137
Ponieważ wartość krytyczna F> wartość F nie można odrzucić hipotezy zerowej.
Wyjaśnienie
W powyższych przykładach widzieliśmy zastosowanie testu F i sposobu jego wykonywania. Ale istnieje zestaw założeń, że musimy zachować ostrożność przed wykonaniem testu F, w przeciwnym razie nie uzyskamy wymaganych wyników:
- Pierwszą rzeczą jest to, że musimy zawsze umieszczać wyższy licznik wartości wariancji podczas obliczania wartości F. Więc jeśli F = V1 / V2, V1 powinno być> V2
- Jeśli chcemy wykonać test 2 ogona, musimy podzielić poziom istotności przez 2, a to będzie odpowiedni poziom, aby znaleźć wartość krytyczną
- Używamy tylko wariancji do obliczania wartości F i jeśli otrzymujemy odchylenia standardowe, jak w przykładzie 2, muszą one zostać podniesione do kwadratu, aby znaleźć wariancję.
- Obie próbki powinny być od siebie niezależne, a wielkość próbki powinna być mniejsza niż 30
- Zestawy populacji, z których pobierane są próbki, muszą być normalnie rozdzielone
Są to kluczowe parametry / założenia, na które należy zwrócić uwagę podczas wykonywania testu F.
Istotność i zastosowanie wzoru F-Test
Test F, jak omówiono powyżej, pomaga nam sprawdzić równość dwóch wariantów populacji. Kiedy więc mamy dwie niezależne próbki, które pochodzą z normalnej populacji i chcemy sprawdzić, czy mają taką samą zmienność, używamy testu F. Test F ma również duże znaczenie w analizie regresji, a także w testowaniu znaczenia R2. Podsumowując, test F jest bardzo ważnym narzędziem w statystyce, jeśli chcemy porównać wariant 2 lub więcej zestawów danych. Ale przed wykonaniem tego testu należy pamiętać o wszystkich założeniach.
Polecane artykuły
To był przewodnik po formule F-Test. Tutaj omawiamy sposób obliczania F-Testu wraz z praktycznymi przykładami i szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- T Formuła dystrybucji
- Wzór na wycenę obligacji
- Formuła błędu procentowego
- Obliczanie wzoru NOPAT