
Wprowadzenie do funkcji sumowania w Matlabie
MATLAB to język używany w informatyce technicznej. Jak większość z nas się zgodzi, łatwe w użyciu środowisko jest koniecznością do integracji zadań obliczeniowych, wizualizacji i wreszcie programowania. MATLAB robi to samo, zapewniając środowisko, które jest nie tylko łatwe w użyciu, ale także rozwiązania, które otrzymujemy, są wyświetlane w kategoriach notacji matematycznych, które są znane większości z nas. W tym artykule przyjrzymy się dokładniej funkcji Sum w Matlabie.
Zastosowania Matlaba obejmują (ale nie tylko)
- Obliczenie
- Opracowanie algorytmów
- Modelowanie
- Symulacja
- Prototypowanie
- Analiza danych (analiza i wizualizacja danych)
- Grafika inżynierska i naukowa
- Rozwój aplikacji
MATLAB zapewnia użytkownikowi koszyk funkcji, w tym artykule zrozumiemy potężną funkcję o nazwie „Funkcja sumowania”.
Składnia:
S = sum(A)
S = sum(A, dim)
S = sum(A, vecdim)
S = sum(__, outtype)
S = sum(__, nanflag)
Opis funkcji sumy w Matlabie
Teraz zrozumiemy wszystkie te funkcje jeden po drugim.
1. S = suma (A)
- Zwróci to sumę wszystkich elementów „A” wzdłuż wymiaru tablicy, który nie jest singletonem, tzn. Rozmiar nie jest równy 1 (weźmie pod uwagę pierwszy wymiar, który nie jest singletonem).
- sum (A) zwróci sumę elementów, jeśli A jest wektorem.
- suma (A) zwróci wektor wiersza, który będzie miał część każdej kolumny, jeśli A jest macierzą.
- Jeśli A jest tablicą wielowymiarową, suma (A) będzie działać wzdłuż pierwszego wymiaru tablicy, którego rozmiar nie jest równy 1 i będzie traktować wszystkie elementy jak wektory. Ten wymiar stanie się 1, a rozmiar innych wymiarów nie zostanie zmieniony.
Teraz zrozumiemy sumę (A) z przykładem. Ale wcześniej pamiętaj, że w MATLAB macierze mają następujące wymiary:
1 = wiersze, 2 = kolumny, 3 = głębokość
Przykład 1 - Gdy mamy zarówno wiersze, jak i kolumny
Jak wyjaśniono powyżej, suma (A) dokona dodania wzdłuż pierwszego wymiaru, który nie jest singletonem. W przypadku pojedynczego wiersza / kolumny otrzymamy wynik w postaci jednej liczby.
A = (1, 3, 7 ; 5, -8, 1);
S = sum(A);
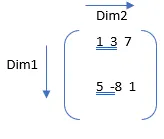
Tutaj 1 jest pierwszym wymiarem nie będącym singletonem (wymiar, którego długość nie jest równa 1). Tak więc niektóre będą wraz z elementami wiersza, tj. Spadną.
S = suma (A) = 6 -5 8
Przykład # 2 - Gdy mamy tylko 1 wiersz
A = (2, 3, 7 );
B = sum(A);
Tutaj pierwszym wymiarem nie będącym singletonem jest 2 (tj. Kolumny). Tak więc suma będzie wraz z elementami kolumny
B = suma (A) = 12
Przykład # 3 - Gdy mamy tylko 1 kolumnę
A = (2 ; 5);
A więc A =
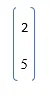
Tutaj pierwszym wymiarem nie będącym singletonem jest 1, więc suma będzie wraz z elementami wiersza.
B = suma (A) = 7
2. S = suma (A, dim)
Ta funkcja zwróci sumę wzdłuż wymiaru przekazanego w argumencie.
Przykład
A = (2 4 3; 5 3 6; 7 2 5)
A więc A =

S = suma (A, 2)
Podaliśmy tutaj jako argument „2”, więc suma będzie wzdłuż wymiaru 2.
Więc S =
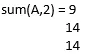
3. S = suma (A, vecdim)
Ta funkcja zsumuje elementy na podstawie wymiarów określonych w wektorze „vecdim”. Na przykład jeśli mamy macierz, wówczas suma (A, (1 2)) będzie sumą wszystkich elementów w A, ponieważ każdy element macierzy A będzie zawarty w wycinku tablicy zdefiniowanym przez wymiary 1 i 2 ( Pamiętaj, że wymiar 1 dotyczy wierszy, a 2 dotyczy kolumn)
Przykład
A = ones(3, 3, 2); (Spowoduje to utworzenie trójwymiarowej tablicy, której wszystkie elementy są równe 1)
Teraz, aby zsumować wszystkie elementy obecne w każdym wycinku macierzy A, musimy określić wymiary, które chcemy zsumować (zarówno wiersz, jak i kolumnę). Możemy to zrobić, podając jako argument wymiar wektorowy. W naszym przykładzie oba wycinki są macierzami 3 * 3, więc suma wyniesie 9.
S1 = suma (A, (1 2))
Zatem S1 = S1 (:, :, 1) = 9
I
S1 (:, :, 2) = 9
4. S = suma (A, typ)
Ta funkcja zwróci sumę z typem danych przekazanym w argumencie. „Typ” może być „natywny”, „domyślny” lub „podwójny”.
Przykład
A = int32(5: 10);
S = sum(A, 'native')
Wyjściem z tego będzie
S = int32
45
Gdzie int32 jest rodzimym typem danych elementów A, a 45 to suma elementów od 5 do 10.
5. S = suma (nanflag)
Określi to, czy musimy uwzględnić lub pominąć NaN w naszych obliczeniach.
suma (A, „includeenan”) obejmie wszystkie wartości NaN, które są obecne w obliczeniach.
sum (A, „omitnan”) zignoruje wszystkie wartości NaN.
Przykład
A = (1 -5 3 -2 NaN 4 NaN 9);
S = sum(A, 'omitnan')
Tak więc wynik, który otrzymamy, to
S = 10
(Po zignorowaniu wszystkich wartości NaN)
Wniosek
Jak więc widzimy, MATLAB jest systemem, którego podstawowym elementem danych jest tablica, która nie wymaga wymiarowania. To pozwala nam rozwiązywać problemy obliczeniowe, zwłaszcza problemy z formułami matrycowymi i wektorowymi. Wszystko to odbywa się w znacznie krótszym czasie w porównaniu do pisania programu w skalarnym i nieinteraktywnym języku, takim jak C.
Polecane artykuły
Jest to przewodnik po Sum Function w Matlabie. Tutaj omawiamy zastosowania Matlaba, składnię, przykłady wraz z opisem funkcji sumowania w Matlabie. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej-
- Wektory w Matlabie
- Funkcje przenoszenia w Matlabie
- Operatory Matlaba
- Co to jest Matlab?
- Kompilator Matlab | Aplikacje kompilatora Matlab