Liczby zespolone w MATLAB - Jak wygenerować liczbę zespoloną?

Wprowadzenie do liczb zespolonych w MATLAB

Liczby zespolone są kombinacją liczb rzeczywistych i liczb urojonych w postaci p + qi, gdzie p i q są liczbami rzeczywistymi, a i jest liczbą urojoną. Liczba urojona jest definiowana, gdzie i jest wynikiem równania a 2 = -1. Możemy użyć i lub j do oznaczenia urojonych jednostek. Ponieważ w dowolnych obliczeniach matematycznych używane są liczby zespolone, a Matlab służy głównie do wykonywania obliczeń matematycznych. Tak więc liczby zespolone stanowią ważną część uczenia się Matlaba.

Generowanie liczb zespolonych w MATLAB

Liczby zespolone mogą być tworzone lub deklarowane w Matlabie za pomocą funkcji „złożonej”. Możemy również tworzyć liczby zespolone, znajdując pierwiastek kwadratowy z dowolnej liczby ujemnej. W Matlabie możemy użyć i lub j, aby oznaczyć urojoną część liczby zespolonej.

Przykłady

X = 4 + 5i

Tutaj X jest liczbą zespoloną, która zawiera 2 części, tj. Część rzeczywistą i urojoną. 4 to część rzeczywista, a 5 to część wyobrażona. Możemy znaleźć prawdziwe i urojone części za pomocą funkcji w Matlabie.

a = rzeczywista (X) = 4 (daje to rzeczywistą część liczby zespolonej)
b = imag (X) = 5 (daje to urojoną część liczby zespolonej)
liczba zespolona (6, 7) = 6 + 7i (Ta funkcja służy do tworzenia liczby zespolonej)

Możemy również tworzyć złożone tablice w Matlabie, które można również zadeklarować za pomocą złożonych funkcji.

a = kompleks (x, y)

Istnieją pewne warunki dla xiy, które powinniśmy przestrzegać, podobnie jak xiy nie powinny być pojedyncze ani podwójne. Złożony skalar można utworzyć, jeśli dwa dane wejściowe mają charakter skalarny, np.

X = kompleks (5, 3)
X = 5, 0000 + 3, 0000i

Podobnie można utworzyć wektor złożony, jeśli mamy dwa wejścia jako wektory.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = kompleks (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Możemy stworzyć liczbę zespoloną mającą tylko jeden skalar, taki jak,

X = kompleks (10)
X = 10, 0000 + 0, 0000i

Istnieją pewne warunki, które powinny spełniać argumenty wejściowe i wyjściowe, takie jak:

Argumenty wejściowe zawierają rzeczywiste i urojone części, takie jak x dowolne y. xiy powinny być skalarem, wektorem, macierzą wielowymiarową lub macierzą w MATLAB. Rozmiar xiy powinien być taki sam. Powinny one być tego samego typu danych, ale istnieje kilka wyjątków, takich jak podwójne można stosować z pojedynczym, a liczbę całkowitą można łączyć z podwójnym, który jest skalarny.

Dane wyjściowe tablicy mogą być wektorowe, skalarne, macierzowe lub wielowymiarowe, w zależności od argumentów wejściowych. Rozmiar danych wyjściowych powinien być taki sam jak danych wejściowych. Jeśli argumenty wejściowe są innego rodzaju niż dane wyjściowe są określone przez,

Jeśli jeden z argumentów wejściowych ma charakter pojedynczy, wówczas wynik powinien być również pojedynczy.
Jeśli którykolwiek z argumentów wejściowych jest z natury liczbą całkowitą, wówczas dane wyjściowe powinny być typu danych całkowitoliczbowych.

Możemy sprawdzić, czy matryca jest rzeczywista czy wymyślona, używając funkcji isreal.

Kod:

X = (2+i, 1); Isreal(X)

Wynik:

Kod:

Isreal (X (2))

Wynik:

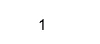
Aby wyodrębnić prawdziwe i urojone części, możemy użyć funkcji rzeczywistych i imag w Matlab, takich jak:

Kod:

real(X)

Wynik:

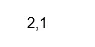
Kod:

imag(X)

Wynik:

Operacje i funkcje liczb zespolonych w MATLAB

Istnieje wiele operacji i funkcji, które można wykonać za pomocą liczb zespolonych w Matlab, takich jak

abs: Ta funkcja służy do znalezienia modułu dowolnej liczby zespolonej w postaci p + qi. abs (2 + 3i) = pierwiastek kwadratowy z (2 2 + 3 2) = (13) 0, 5
kąt: Aby znaleźć kąt fazowy liczby zespolonej.

Istnieją pewne wskazówki, których należy przestrzegać w celu prawidłowego funkcjonowania liczb zespolonych w Matlabie, takich jak:

Powinniśmy unikać używania i ij jako części nazw zmiennych, ponieważ są one używane do oznaczania urojonych części liczby zespolonej.
Powinniśmy unikać używania j lub i, jeśli urojoną częścią jest 1. Zamiast tego możemy użyć 1j lub 1i.
Możemy stworzyć złożoną funkcję w Matlabie, gdy i i j są używane jako nazwy zmiennych w niektórych częściach, argumenty wejściowe nie są pojedynczego lub podwójnego typu, a część urojona wynosi zero.

Wniosek

Liczby zespolone są używane w dziedzinie matematyki lub inżynierii. Wiele rzeczywistych lub praktycznych zastosowań można opisać za pomocą wyobrażonej części liczb zespolonych. Dlatego zrozumienie użycia i zastosowania liczb zespolonych na różnych platformach jest ważne, szczególnie jeśli masz do czynienia z jakąkolwiek dziedziną fizyczną lub matematyczną.

Polecane artykuły

Jest to przewodnik po liczbach zespolonych w MATLAB. Tutaj omawiamy wprowadzenie i generowanie liczb zespolonych w Matlabie, w tym jego przykłady z działaniem i funkcją. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej-