Wprowadzenie do hierarchicznego algorytmu grupowania
Hierarchiczny algorytm grupowania jest techniką uczenia maszynowego bez nadzoru. Ma na celu znalezienie naturalnego grupowania na podstawie cech danych.
Hierarchiczny algorytm grupowania ma na celu znalezienie zagnieżdżonych grup danych poprzez zbudowanie hierarchii. Jest podobny do taksonomii biologicznej królestwa roślin lub zwierząt. Klastry hierarchiczne są ogólnie reprezentowane przy użyciu drzewa hierarchicznego znanego jako dendrogram.
Rodzaje hierarchicznego algorytmu grupowania
Hierarchiczne algorytmy grupowania są dwojakiego rodzaju:
- Dzielący
- Aglomeracyjny
1. Dzielące
Jest to podejście odgórne, w którym początkowo uznaje się wszystkie dane za jedną grupę, a następnie iteracyjnie dzieli dane na podgrupy. Jeśli znana jest liczba hierarchicznych algorytmów klastrowania, wówczas proces podziału zatrzymuje się po osiągnięciu liczby klastrów. W przeciwnym razie proces zatrzymuje się, gdy danych nie można już podzielić, co oznacza, że podgrupa uzyskana z bieżącej iteracji jest taka sama jak ta uzyskana z poprzedniej iteracji (można również uznać, że podział kończy się, gdy każdy punkt danych jest klastrem ).
2. Aglomeracja
Jest to podejście oddolne, które polega na łączeniu się klastrów. Początkowo dane są dzielone na m klastrów singletonowych (gdzie wartość m jest liczbą próbek / punktów danych). Dwa klastry są łączone w jeden iteracyjnie, co zmniejsza liczbę klastrów w każdej iteracji. Ten proces łączenia klastrów kończy się, gdy wszystkie klastry zostaną połączone w jeden lub liczba pożądanych klastrów zostanie osiągnięta.
Na poziomie 1 istnieje m klastrów, które zostają zredukowane do 1 klastra na poziomie m. Te punkty danych, które zostaną scalone w celu utworzenia klastra na niższym poziomie, również pozostają w tym samym klastrze na wyższych poziomach. Np. Załóżmy, że jest 8 punktów x1..x8, więc na początku jest 8 klastrów na poziomie 1. Załóżmy, że punkty x1 i x2 zostaną połączone w klaster na poziomie 2, a następnie do poziomu 8 pozostaną w tym samym klastrze.
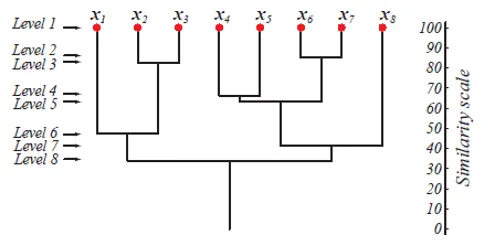
Powyższy rysunek pokazuje dendrogram reprezentujący podejście grupowania aglomeracji dla 8 punktów danych, a także skalę podobieństwa odpowiadającą każdemu poziomowi.
Poziomy klastrów dają nam wyobrażenie o tym, jak podobne są punkty danych w klastrach. Jak pokazano na ryc. 1, wcześniej punkty danych zostają scalone w klaster, tym podobne są. Punkty danych w klastrze na poziomie 2 (np. X2 i x3) są bardziej podobne niż punkty danych w klastrze na poziomie 6 (np. X1 i x2).
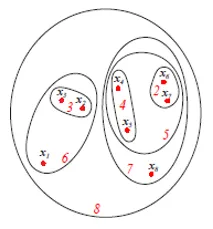
Powyższy rysunek przedstawia schemat Seta lub Venna aglomeracyjnego podejścia grupowania wyżej wymienionych 8 punktów danych. Do grupowania można użyć zarówno dendrogramów, jak i reprezentacji zestawów. Jednak zwykle preferowany jest dendrogram. Reprezentacja zasobów nie może ilościowo reprezentować podobieństw klastrów.
Kroki dla hierarchicznego algorytmu grupowania
Postępujmy zgodnie z następującymi krokami dla hierarchicznego algorytmu klastrowania, które podano poniżej:
1. Algorytm
Aglomeracyjny hierarchiczny algorytm grupowania
- Rozpocznij inicjalizację c, c1 = n, Di = (xi), i = 1, …, n '
- Czy c1 = c1 - 1
- Znajdź najbliższe klastry, powiedzmy Di i Dj
- Scal Di i Dj
- Aż do c = c1
- Zwróć klastry c
- Koniec
Ten algorytm zaczyna się od n klastrów początkowo, w których każdy punkt danych jest klastrem. Z każdą iteracją liczba klastrów zmniejsza się o 1 w miarę łączenia 2 najbliższych klastrów. Proces ten trwa, dopóki liczba klastrów nie spadnie do wstępnie określonej wartości c.
Jak zdecydować, które klastry są w pobliżu?
To jest zdefiniowane przy użyciu kilku wskaźników odległości, które są następujące:
- Minimalna odległość między klastrami dmin (Di, Dj). Przydatny dla singla.
- Maksymalna odległość między klastrami dmax (Di, Dj). Przydatne do ukończenia.
- Średnia odległość między klastrami davg (Di, Dj).
Co to jest pojedyncze połączenie i pełne połączenie?
- Gdy dmin (di, dj) jest używane do znalezienia odległości między dwoma klastrami, a algorytm kończy się, jeśli odległość między najbliższymi klastrami przekracza próg, wówczas algorytm nazywa się algorytmem pojedynczego łączenia.
- Gdy dmax (Di, Dj) jest używane do znalezienia odległości między dwoma klastrami, a algorytm kończy się, jeśli odległość między najbliższymi klastrami przekracza próg, wówczas algorytm nazywany jest kompletnym algorytmem łączenia.
- Rozważmy każdy punkt danych jako węzeł wykresu. Pomiędzy dwoma punktami danych występuje krawędź, jeśli należą one do tego samego klastra. Po scaleniu dwóch najbliższych klastrów dodawana jest krawędź. Nazywa się to pojedynczym połączeniem, ponieważ istnieje unikalna ścieżka od jednego węzła do drugiego.
- Kompletny algorytm łączenia łączy dwa klastry, minimalizując odległość między dwoma najdalszymi punktami.
- Pojedynczy algorytm łączenia generuje drzewo opinające. Jednak ten algorytm jest podatny na zakłócenia. Kompletny algorytm łączenia generuje pełny wykres.
Jaka jest złożoność czasowa algorytmu?
Załóżmy, że mamy n wzorów w przestrzeni d-wymiarowej i używamy dmin (Di, Dj) do tworzenia klastrów c. Musimy obliczyć n (n - 1) odległości między punktami - z których każda jest obliczeniem O (d 2 ) - i umieścić wyniki w tabeli odległości między punktami. Złożoność przestrzeni wynosi O (n 2 ). Znalezienie minimalnej pary odległości (dla pierwszego scalenia) wymaga przejścia przez całą listę, zachowując indeks najmniejszej odległości.
Zatem dla pierwszego etapu aglomeracji złożoność wynosi O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). W przypadku kolejnego arbitralnego kroku aglomeracji (tj. Od c1 do c1 - 1), po prostu przechodzimy przez „nieużywane” odległości n (n - 1) - c1 na liście i znajdujemy najmniejsze, dla których x i x 'leżą w różnych klastrach . To znowu O (n (n − 1) −c1). Całkowity czas złożoności wynosi zatem O (cn 2 d 2 ), aw typowych warunkach n >> c.
2. Wizualizacja
Po podzieleniu danych na klastry dobrą praktyką jest wizualizacja klastrów, aby uzyskać wyobrażenie o tym, jak wygląda grupowanie. Ale wizualizacja tych wysokowymiarowych danych jest trudna. Dlatego do wizualizacji używamy analizy głównych składników (PCA). Po PCA uzyskujemy punkty danych w przestrzeni niskiego wymiaru (zazwyczaj 2D lub 3D), które możemy narysować, aby zobaczyć grupowanie.
Uwaga: Wysoki wymiar oznacza dużą liczbę funkcji, a nie liczbę punktów danych.3. Ocena
Jedną z metod oceny klastrów jest to, że odległość punktów między klastrami (odległość między klastrami) powinna być znacznie większa niż odległość punktów w klastrze (odległość wewnątrz klastra).
Wniosek
Oto kilka kluczowych rzeczy na wynos:
- Hierarchiczny algorytm grupowania służy do znajdowania zagnieżdżonych wzorców w danych
- Hierarchiczne grupowanie jest dwojakiego rodzaju - dzielące i aglomeracyjne
- Do reprezentacji można użyć Dendrogramu i diagramu set / Venna
- Pojedyncze połączenie łączy dwa klastry, minimalizując minimalną odległość między nimi. Tworzy połączenie
- Kompletne połączenie łączy dwa klastry, minimalizując maksymalną odległość między nimi, tworząc pełny wykres.
- Całkowity czasowo złożoność hierarchicznego algorytmu grupowania wynosi O (cn 2 d 2 ), gdzie c jest predefiniowaną liczbą klastrów, n jest liczbą wzorców, a d jest przestrzenią d wymiarów n wzorców.
Polecane artykuły
Jest to przewodnik po algorytmie hierarchicznego grupowania. Tutaj omawiamy typy i kroki hierarchicznych algorytmów klastrowych. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej-
- Hierarchiczna analiza skupień
- Hierarchiczne grupowanie w R '
- Algorytm grupowania
- Co to jest klastrowanie w eksploracji danych?
- Hierarchiczne grupowanie | Grupowanie aglomeracyjne i dzielące
- Algorytm C ++ | Przykłady algorytmu C ++