Skorygowana formuła R do kwadratu (spis treści)
- Skorygowano formułę R do kwadratu
- Przykłady skorygowanej formuły R do kwadratu (z szablonem Excel)
Skorygowano formułę R do kwadratu
Zanim przejdziemy do skorygowanej formuły r do kwadratu, musimy zrozumieć, czym jest R2. W statystyce R2 znany również jako współczynnik determinacji jest narzędziem, dla którego określa i ocenia zmienność zmiennej zależnej, co tłumaczy się zmienną niezależną w modelu statystycznym. Więc jeśli R2 jest powiedziane 0, 6, oznacza to, że 60% zmian w zmiennej zależnej jest wyjaśnione przez zmienną niezależną. Ale problem z R2 polega na tym, że jego wartość rośnie wraz z dodawaniem większej liczby zmiennych, niezależnie od znaczenia tej zmiennej. Aby temu zaradzić, wprowadzono koncepcję skorygowanego kwadratu r. Idea stojąca za R 2 i skorygowanym R Squared jest taka sama, ale różnica polega na tym, że skorygowany r Squared dostosowuje wartość r kwadratową dla liczby wyrażeń w modelu.
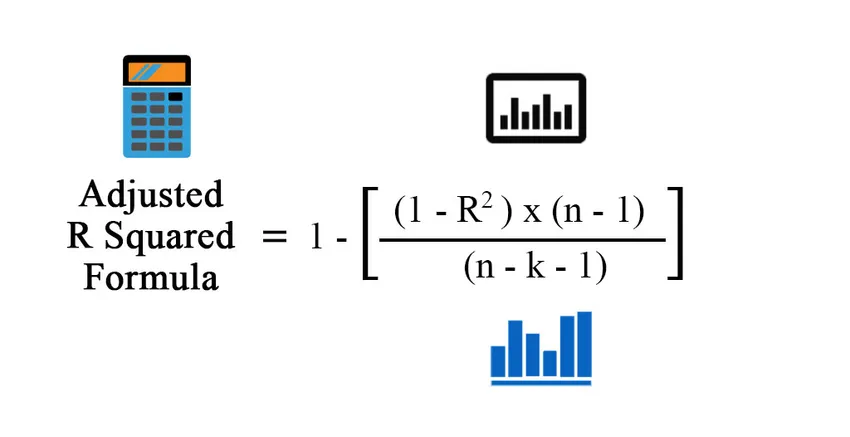
Formuła skorygowanego kwadratu R:
Zanim obliczymy skorygowane r do kwadratu, najpierw musimy r kwadrat. Istnieją różne sposoby obliczania kwadratu r:
- Za pomocą współczynnika korelacji:
Współczynnik korelacji = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
Gdzie:
- X - Punkty danych w zbiorze danych X
- Y - Punkty danych w zbiorze danych Y
- X m - Średnia zbioru danych X
- Y m - Średnia zbioru danych Y
Więc
R 2 = (współczynnik korelacji) 2
Adjusted R Squared = 1 – (((1 – R 2 ) * (n – 1)) / (n – k – 1))
Gdzie:
- n - liczba punktów w zbiorze danych.
- k - Liczba zmiennych niezależnych w modelu, z wyłączeniem stałej
- Korzystanie z wyników regresji
R 2 = Zmiana wyjaśniona / Zmiana całkowita
R2 = MSS / TSS
R 2 = (TSS - RSS) / TSS
Gdzie:
- TSS - suma kwadratów = Σ (Yi - Ym) 2
- MSS - Modelowa suma kwadratów = Σ (Y - Ym) 2
- RSS - Resztkowa suma kwadratów = Σ (Yi - Y ^) 2
Y to przewidywana wartość modelu, Yi to i-ta wartość, a Ym to wartość średnia
Adjusted R Squared = 1 – (((1 – R 2 ) * (n – 1)) / (n – k – 1))
Przykłady skorygowanej formuły R do kwadratu (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczenie skorygowanego kwadratu R.
Możesz pobrać ten dostosowany szablon Excel Formula R Squared Formula - dostosowany szablon Excel Formula R SquaredSkorygowana formuła R do kwadratu - przykład nr 1
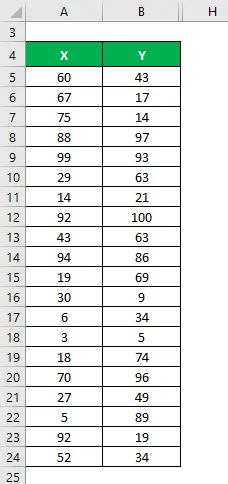
Załóżmy, że mamy dwa zestawy danych X i Y, z których każdy zawiera 20 losowych punktów danych. Obliczyć skorygowane R do kwadratu dla zestawu danych X i Y.
Średnia jest obliczana jako:
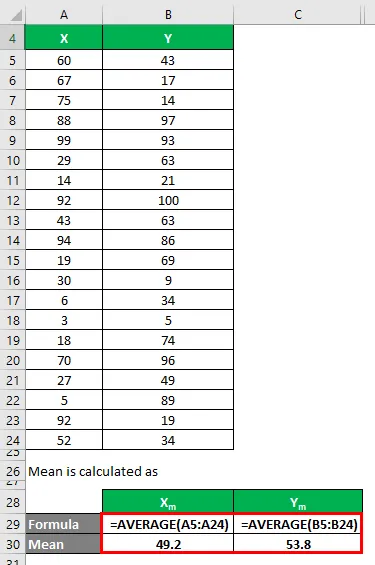
- Średnia zbioru danych X = 49, 2
- Średnia zbioru danych Y = 53, 8
Teraz musimy obliczyć różnicę między punktami danych a wartością średnią.
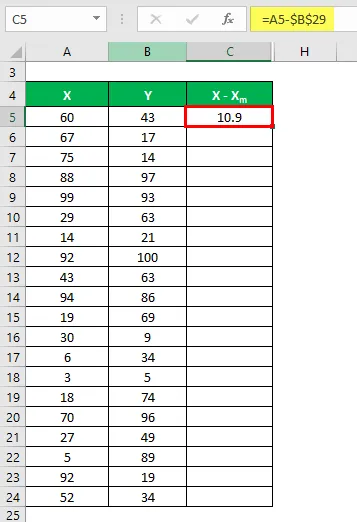
Podobnie obliczyć dla wszystkich zestawów danych X.
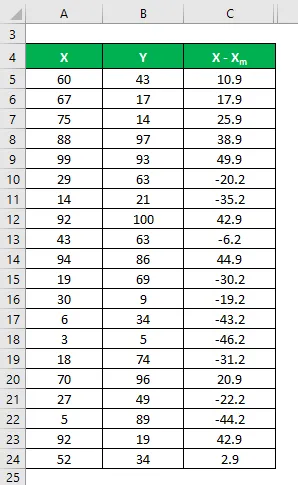
Podobnie obliczyć go również dla zbioru danych Y.
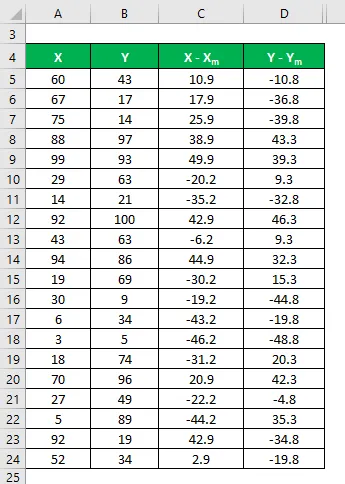
Oblicz kwadrat różnicy dla obu zestawów danych X i Y.
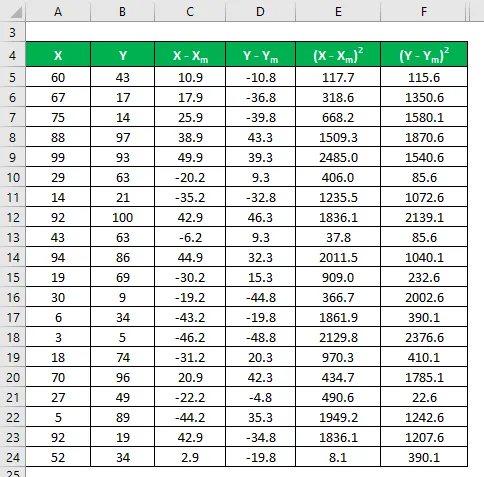
Pomnóż różnicę w X przez Y.
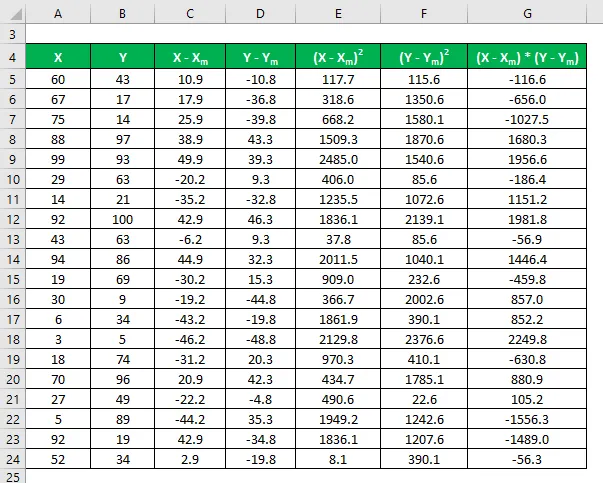
Współczynnik korelacji oblicza się przy użyciu poniższego wzoru
Współczynnik korelacji = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
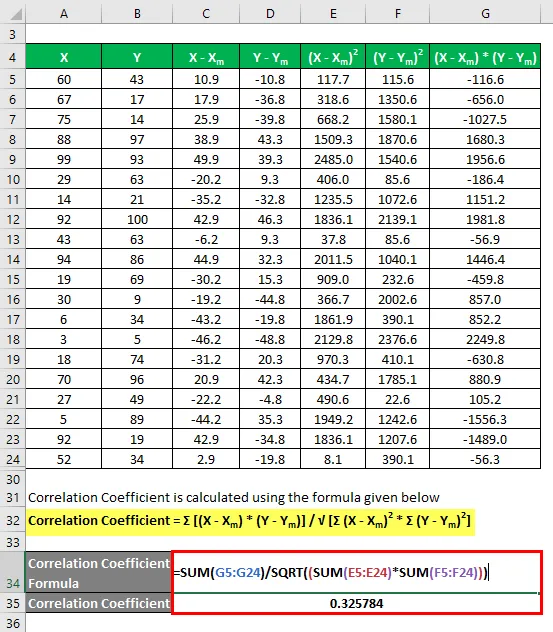
Współczynnik korelacji = 0, 325784
R2 oblicza się przy użyciu poniższego wzoru
R 2 = (współczynnik korelacji) 2
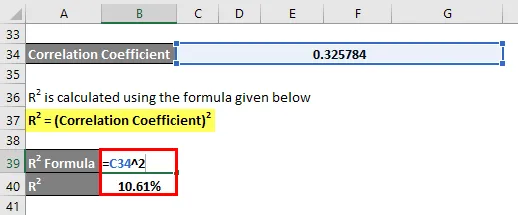
R 2 = 10, 61%
Skorygowane R do kwadratu jest obliczane przy użyciu wzoru podanego poniżej
Skorygowane R Kwadrat = 1 - (((1 - R 2 ) * (n - 1)) / (n - k - 1))
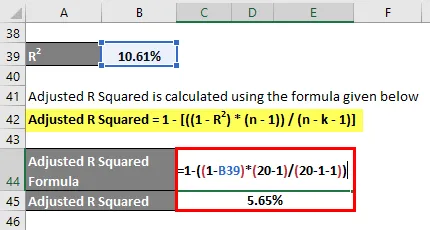
- Skorygowane R Kwadrat = 1 - ((1 - 10, 61%) * (20 - 1) / (20 - 1 - 1))
- Skorygowane R Kwadrat = 5, 65%
Skorygowana formuła R do kwadratu - przykład # 2
Użyjmy innej metody do obliczenia kwadratu r, a następnie skorygowanego kwadratu r. Powiedzmy, że masz przy sobie rzeczywiste i przewidywane wartości zmiennych zależnych (Y i Y ^):
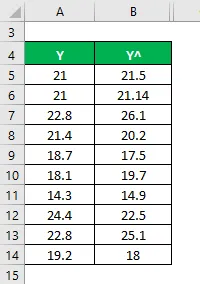
Średnia jest obliczana jako
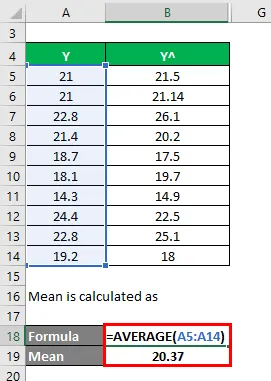
Teraz musimy obliczyć różnicę między rzeczywistymi a przewidywanymi wartościami zmiennych zależnych.
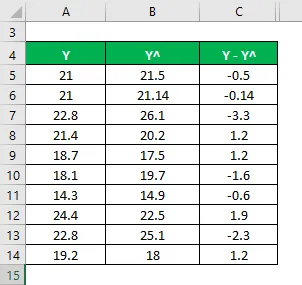
Obliczyć różnicę między punktami danych a wartością średnią.
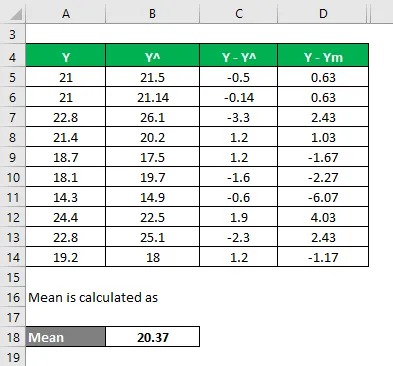
Oblicz kwadrat różnic.
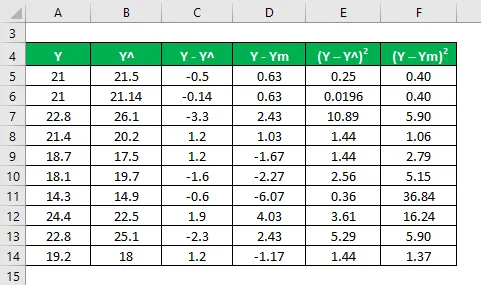
R2 oblicza się przy użyciu poniższego wzoru
R 2 = (TSS - RSS) / TSS
- TSS = Σ (Y - Ym) 2
- RSS = Σ (Y - Y ^) 2
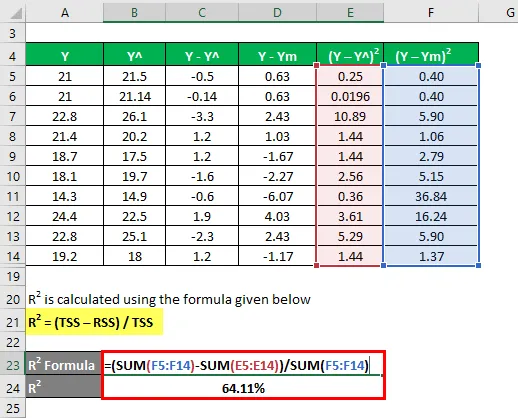
R 2 = 64, 11%
Powiedzmy teraz, że mamy 3 niezależne zmienne: tj. K = 3.
Skorygowane R do kwadratu jest obliczane przy użyciu wzoru podanego poniżej
Skorygowane R Kwadrat = 1 - (((1 - R 2 ) * (n - 1)) / (n - k - 1))
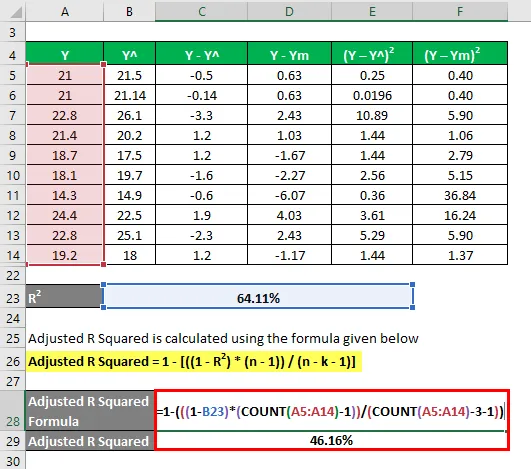
- Skorygowane R Kwadrat = 1 - (((1 - 64, 11%) * (10-1)) / (10 - 3 - 1))
- Skorygowane R Kwadrat = 46, 16%
Wyjaśnienie
R2 lub współczynnik determinacji, jak wyjaśniono powyżej, jest kwadratem korelacji między 2 zestawami danych. Jeśli R2 wynosi 0, oznacza to, że nie ma korelacji, a zmienna niezależna nie może przewidzieć wartości zmiennej zależnej. Podobnie, jeśli jego wartość wynosi 1, oznacza to, że zmienna niezależna zawsze odniesie sukces w przewidywaniu zmiennej zależnej. Ale są też pewne ograniczenia. Wraz ze wzrostem liczby zmiennych niezależnych w modelu statystycznym, R 2 zwiększa się również, czy te nowe zmienne mają sens, czy nie. To jest powód, dla którego skorygowane r kwadrat jest obliczane, ponieważ dostosowuje wartość R2 dla tego wzrostu wielu zmiennych. Skorygowana wartość kwadratu zmniejsza się, jeśli ta zmienna niezależna nie jest znacząca, i rośnie, jeśli ma to znaczenie.
Trafność i zastosowania skorygowanej formuły R do kwadratu
Skorygowany kwadrat r jest bardziej użyteczny, gdy mamy więcej niż 1 zmienne niezależne, ponieważ dostosowuje kwadrat r i bierze pod uwagę tylko odpowiednią zmienną niezależną, co faktycznie tłumaczy zmianę w zmiennej zależnej. Jego wartość jest zawsze mniejsza niż wartość R2. Ogólnie rzecz biorąc, istnieje wiele praktycznych zastosowań tego narzędzia, takich jak porównanie wyników portfela z prognozami rynkowymi i przyszłymi, modelowanie ryzyka w funduszach hedgingowych itp.
Polecane artykuły
To był przewodnik po skorygowanej formule R do kwadratu. Tutaj omawiamy sposób obliczania skorygowanego kwadratu R wraz z praktycznymi przykładami i szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przykłady wzoru kalkulacji absorpcji
- Przewodnik po formule stopnia dźwigni finansowej
- Formuła do obliczania wyceny obligacji
- Formuła rozkładu dwumianowego