Różnica między regresją liniową a regresją logistyczną
Poniższy artykuł Regresja liniowa a regresja logistyczna przedstawia najważniejsze różnice między nimi, ale zanim zobaczymy, co oznacza regresja?
Regresja
Regresja jest w zasadzie miarą statystyczną służącą do określenia siły zależności między jedną zmienną zależną, tj. Wyjściem Y i szeregiem innych zmiennych niezależnych, tj. X 1, X 2 i tak dalej. Analiza regresji jest zasadniczo używana do prognozowania i prognozowania.
Co to jest regresja liniowa?
Regresja liniowa jest algorytmem opartym na nadzorowanej dziedzinie uczenia maszynowego. Dziedziczy liniową zależność między zmiennymi wejściowymi a pojedynczą zmienną wyjściową, przy czym zmienna wyjściowa ma charakter ciągły. Służy do przewidywania wartości wyjściowej, powiedzmy Y z danych wejściowych, powiedzmy X. Gdy rozważane jest tylko pojedyncze wejście, nazywa się to prostą regresją liniową.
Można go podzielić na dwie główne kategorie:
1. Prosta regresja
Zasada działania: Głównym celem jest znalezienie równania linii prostej, która najlepiej pasuje do próbkowanych danych. To równanie algebraicznie opisuje związek między dwiema zmiennymi. Najlepiej pasująca linia prosta nazywana jest linią regresji.
Y = β 0 + β 1 X
Gdzie,
β reprezentuje cechy
β 0 oznacza punkt przecięcia
β 1 reprezentuje współczynnik cechy X
2. Regresja wielowymiarowa
Służy do przewidywania korelacji między więcej niż jedną zmienną niezależną a jedną zmienną zależną. Regresja z więcej niż dwiema niezależnymi zmiennymi opiera się na dopasowaniu kształtu do konstelacji danych na wykresie wielowymiarowym. Kształt regresji powinien być taki, aby minimalizował odległość kształtu od każdego punktu danych.
Model zależności liniowej można przedstawić matematycznie, jak poniżej:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Gdzie,
β reprezentuje cechy
β 0 oznacza punkt przecięcia
β 1 reprezentuje współczynnik cechy X 1
β n reprezentuje współczynnik cechy X n
Zalety i wady regresji liniowej
Poniżej podano zalety i wady:
Zalety
- Ze względu na swoją prostotę jest szeroko stosowany do modelowania prognoz i wniosków.
- Koncentruje się na analizie danych i ich wstępnym przetwarzaniu. Więc zajmuje się różnymi danymi bez zawracania sobie głowy szczegółami modelu.
Niedogodności
- Działa skutecznie, gdy dane są zwykle dystrybuowane. Dlatego w celu skutecznego modelowania należy unikać kolinearności.
Co to jest regresja logistyczna?
Jest to forma regresji, która pozwala przewidywać zmienne dyskretne na podstawie kombinacji predyktorów ciągłych i dyskretnych. Powoduje to unikalną transformację zmiennych zależnych, która wpływa nie tylko na proces estymacji, ale także na współczynniki zmiennych niezależnych. Odnosi się do tego samego pytania, co regresja wielokrotna, ale bez założeń dystrybucyjnych dotyczących predyktorów. W regresji logistycznej zmienna wynikowa jest binarna. Celem analizy jest ocena skutków wielu zmiennych objaśniających, które mogą być liczbowe lub kategoryczne, lub obu.
Rodzaje regresji logistycznej
Poniżej znajdują się 2 typy regresji logistycznej:
1. Binarna regresja logistyczna
Jest używany, gdy zmienna zależna jest dychotomiczna, tj. Jak drzewo z dwiema gałęziami. Jest stosowany, gdy zmienna zależna jest nieparametryczna.
Używane, gdy
- Jeśli nie ma liniowości
- Istnieją tylko dwa poziomy zmiennej zależnej.
- Jeśli normalność na wielu odmianach jest wątpliwa.
2. Wielomianowa regresja logistyczna
Analiza wielomianowej regresji logistycznej wymaga, aby zmienne niezależne były metryczne lub dychotomiczne. Nie przyjmuje żadnych założeń liniowości, normalności i jednorodności wariancji dla zmiennych niezależnych.
Jest używany, gdy zmienna zależna ma więcej niż dwie kategorie. Służy do analizy zależności między niemetryczną zmienną zależną od metrycznych lub dychotomicznych zmiennych niezależnych, a następnie porównuje wiele grup za pomocą kombinacji binarnych regresji logistycznych. Na koniec zapewnia zestaw współczynników dla każdego z dwóch porównań. Współczynniki dla grupy referencyjnej są przyjmowane jako wszystkie zera. Wreszcie prognozowanie odbywa się na podstawie najwyższego prawdopodobieństwa wypadkowego.
Zaleta regresji logistycznej: Jest to bardzo wydajna i szeroko stosowana technika, ponieważ nie wymaga wielu zasobów obliczeniowych i nie wymaga strojenia.
Wada regresji logistycznej: nie można jej używać do rozwiązywania problemów nieliniowych.
Bezpośrednie porównanie regresji liniowej z regresją logistyczną (infografiki)
Poniżej znajduje się 6 najważniejszych różnic między regresją liniową a regresją logistyczną 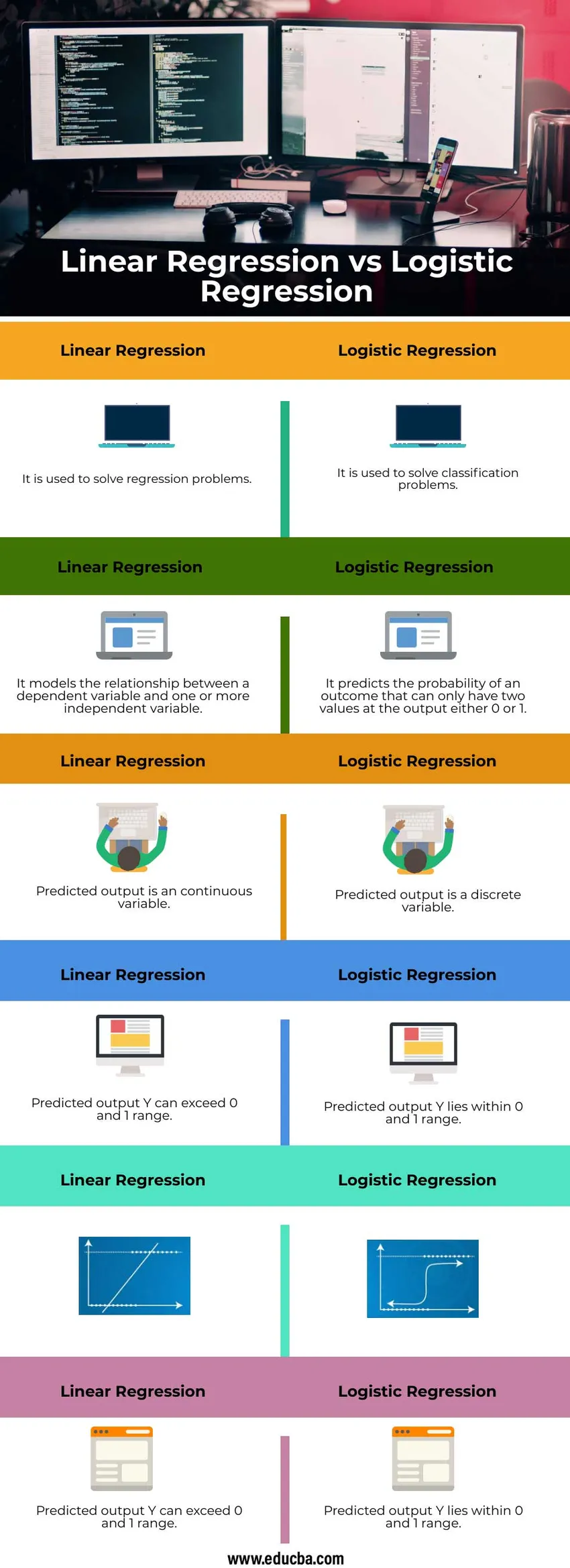
Kluczowa różnica między regresją liniową a regresją logistyczną
Omówmy niektóre z głównych kluczowych różnic między regresją liniową a regresją logistyczną
Regresja liniowa
- Jest to podejście liniowe
- Używa linii prostej
- Nie może przyjmować zmiennych kategorialnych
- Musi ignorować obserwacje z brakującymi wartościami liczbowej zmiennej niezależnej
- Wyjście Y podano jako
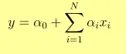
- Wzrost o 1 jednostkę x zwiększa Y o α
Aplikacje
- Prognozowanie ceny produktu
- Przewidywanie wyniku w meczu
Regresja logistyczna
- To podejście statystyczne
- Wykorzystuje funkcję sigmoidalną
- Może przyjmować zmienne jakościowe
- Może podejmować decyzje, nawet jeśli obecne są obserwacje z brakującymi wartościami
- Wyjście Y podano jako, gdzie z podano jako
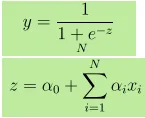
- Wzrost o 1 jednostkę x zwiększa Y o logarytmiczne szanse α
- Jeśli P jest prawdopodobieństwem zdarzenia, to (1-P) oznacza prawdopodobieństwo jego wystąpienia. Szanse powodzenia = P / 1-P
Aplikacje
- Przewidywanie, czy dzisiaj będzie padać, czy nie.
- Przewidywanie, czy wiadomość e-mail jest spamem, czy nie.
Tabela porównawcza regresji liniowej a regresja logistyczna
Omówmy najlepsze porównanie między regresją liniową a regresją logistyczną
|
Regresja liniowa |
Regresja logistyczna |
| Służy do rozwiązywania problemów regresji | Służy do rozwiązywania problemów z klasyfikacją |
| Modeluje związek między zmienną zależną a jedną lub większą liczbą zmiennych niezależnych | Przewiduje prawdopodobieństwo wyniku, który może mieć tylko dwie wartości na wyjściu 0 lub 1 |
| Przewidywana moc wyjściowa jest zmienną ciągłą | Przewidywana moc wyjściowa jest zmienną dyskretną |
| Przewidywana moc wyjściowa Y może przekraczać zakres 0 i 1 | Przewidywana moc wyjściowa Y mieści się w zakresie 0 i 1 |
 | 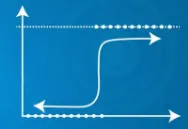 |
| Przewidywana moc wyjściowa Y może przekraczać zakres 0 i 1 | Przewidywana moc wyjściowa |
Wniosek
Jeśli cechy nie przyczyniają się do przewidywania lub jeśli są ze sobą bardzo skorelowane, to dodaje szum do modelu. Tak więc funkcje, które nie przyczyniają się wystarczająco do modelu, muszą zostać usunięte. Jeśli zmienne niezależne są wysoce skorelowane, może to powodować problem wielokolinearności, który można rozwiązać, uruchamiając osobne modele dla każdej zmiennej niezależnej.
Polecane artykuły
Jest to przewodnik po regresji liniowej a regresji logistycznej. Omawiamy tutaj różnice między regresją liniową a regresją logistyczną z infografiką i tabelą porównawczą. Możesz także zapoznać się z następującymi artykułami, aby dowiedzieć się więcej -
- Nauka danych a wizualizacja danych
- Uczenie maszynowe a sieć neuronowa
- Uczenie nadzorowane a uczenie głębokie
- Regresja logistyczna w R.