
Wprowadzenie do rozkładu dwumianowego w R.
W tym artykule opisano, jak używać rozkładów dwumianowych w R dla kilku operacji związanych z rozkładami prawdopodobieństwa. Analiza biznesowa wykorzystuje prawdopodobieństwo dwumianowe dla złożonego problemu. R ma wiele wbudowanych funkcji do obliczania rozkładów dwumianowych wykorzystywanych w interferencji statystycznej. Rozkład dwumianowy znany również jako próby Bernoulliego wymaga dwóch rodzajów sukcesu p i niepowodzenia S. Głównym celem modelu rozkładu dwumianowego jest obliczenie możliwych wyników prawdopodobieństwa poprzez monitorowanie określonej liczby pozytywnych możliwości poprzez powtarzanie procesu określoną liczbę razy . Powinny mieć dwa możliwe wyniki (sukces / porażka), dlatego wynik jest dychotomiczny. Wstępnie zdefiniowanym zapisem matematycznym jest p = sukces, q = 1-p.
Istnieją cztery funkcje związane z rozkładami dwumianowymi. Są to dbinom, pbinom, qbinom, rbinom. Sformatowana składnia jest podana poniżej:
Składnia
- dbinom (x, rozmiar, prob)
- pbinom (x, rozmiar, prob)
- qbinom (x, size, prob) lub qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, rozmiar, prob)
Funkcja ma trzy argumenty: wartość x jest wektorem kwantyli (od 0 do n), rozmiar jest liczbą prób śladu, prob oznacza prawdopodobieństwo każdej próby. Zobaczmy jeden po drugim z przykładem.
1) dbinom ()
Jest to funkcja gęstości lub rozkładu. Wartości wektorowe muszą być liczbą całkowitą, nie powinna być liczbą ujemną. Ta funkcja próbuje znaleźć szereg sukcesów na nie. ustalonych prób.
Rozkład dwumianowy przyjmuje wartości wielkości i x. na przykład rozmiar = 6, możliwe wartości x wynoszą 0, 1, 2, 3, 4, 5, 6, co implikuje P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Wynik:
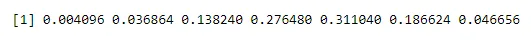
Prawdopodobieństwo do jednego
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Wynik:
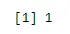
Przykład 1 - Baza danych szpitala pokazuje, że pacjenci cierpiący na raka, 65% umiera z tego powodu. Jakie jest prawdopodobieństwo, że 5 losowo wybranych pacjentów, z których 3 wyzdrowieje?
Tutaj stosujemy funkcję dbinom. Prawdopodobieństwo, że 3 wyzdrowieje przy użyciu rozkładu gęstości we wszystkich punktach.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Wynik:

Dla wartości x od 0 do 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Wynik:
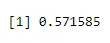
Następnie utwórz próbkę 40 papierów i zwiększaj o 2, również tworząc dwumian za pomocą dbinom.
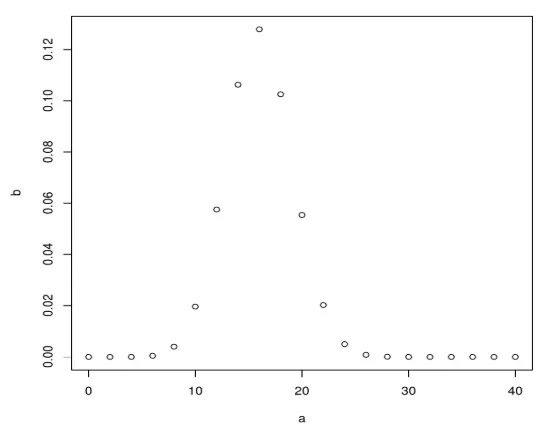
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Po wykonaniu powyższego kodu generuje następujące dane wyjściowe: Rozkład dwumianowy jest wykreślany za pomocą funkcji plot ().
Przykład 2 - Rozważmy scenariusz, załóżmy, że prawdopodobieństwo pożyczenia przez ucznia książki z biblioteki wynosi 0, 7. W bibliotece jest 6 uczniów, jakie jest prawdopodobieństwo, że 3 z nich pożyczy książkę?
tutaj P (X = 3)
Kod:
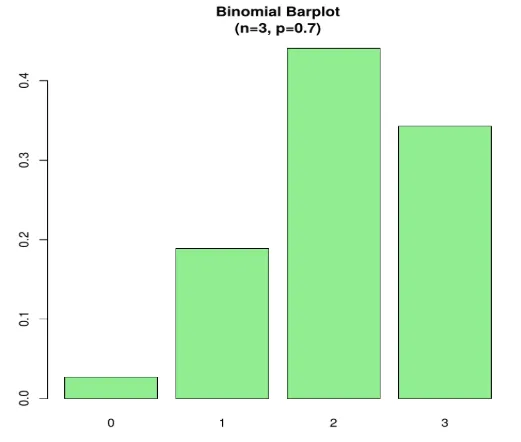
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Wykres poniżej pokazuje, gdy p> 0, 5, dlatego rozkład dwumianowy jest dodatnio przekrzywiony, jak pokazano.
Wynik:
2) Pbinom ()
oblicza skumulowane prawdopodobieństwa dwumianowe lub CDF (P (X <= x)).
Przykład 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Wynik:

Przykład 2: Dravid zdobywa furtkę w 20% swoich prób, gdy rzuca kręgle. Jeśli rzuca 5 razy w kręgle, jakie byłoby prawdopodobieństwo, że zdobędzie 4 lub mniej bramek?
Prawdopodobieństwo sukcesu wynosi tutaj 0, 2 i podczas 5 prób otrzymujemy
pbinom(4, size=5, prob=.2)
Wynik:
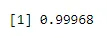
Przykład 3: 4% Amerykanów to Czarni. Znajdź prawdopodobieństwo 2 czarnych studentów przy losowym wybieraniu 6 uczniów z klasy 100 bez zamiany.
Gdy R: x = 4 R: n = 6 R: p = 0, 0 4
pbinom(4, 6, 0.04)
Wynik:-
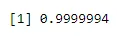
3) qbinom ()
Jest to funkcja kwantylowa, która wykonuje odwrotność funkcji skumulowanego prawdopodobieństwa. Skumulowana wartość odpowiada wartości prawdopodobieństwa.
Przykład: ile ogonów będzie miało prawdopodobieństwo 0.2, gdy moneta zostanie rzucona 61 razy.
a <- qbinom(0.2, 61, 1/2)
print(a)
Wynik:-
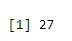
4) rbinom ()
Generuje losowe liczby. Różne wyniki dają różne losowe wyniki, wykorzystywane w procesie symulacji.
Przykład:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Wynik:-

Za każdym razem, gdy wykonujemy, daje losowe wyniki.
rbinom(200, 4, 0.4)
Wynik:-

Tutaj robimy to, zakładając wynik 30 rzutów monetą za jednym razem.
rbinom(30, 1, 0.5)
Wynik:-
Korzystanie z wykresu słupkowego:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Wynik:-
Aby znaleźć sposób na sukces
output <-rbinom(10, size=60, 0.3)
mean(output)
Wynik:-
Wniosek - rozkład dwumianowy w R.
Dlatego w tym dokumencie omówiliśmy rozkład dwumianowy w R. Symulowaliśmy na różnych przykładach w studio R i we fragmentach R, a także opisaliśmy wbudowane funkcje pomocne w generowaniu obliczeń dwumianowych. Obliczenia rozkładu dwumianowego w R wykorzystują obliczenia statystyczne. Dlatego rozkład dwumianowy pomaga znaleźć prawdopodobieństwo i losowe wyszukiwanie przy użyciu zmiennej dwumianowej.
Polecane artykuły
To jest przewodnik po rozkładzie dwumianowym w R. Omówiliśmy wprowadzenie i jego funkcje związane z rozkładem dwumianowym wraz ze składnią i odpowiednimi przykładami. Możesz także przejrzeć nasze inne sugerowane artykuły, aby dowiedzieć się więcej -
- Formuła rozkładu dwumianowego
- Ekonomia kontra biznes
- Techniki analityki biznesowej
- Dystrybucje systemu Linux