Wprowadzenie do drzewa AVL w strukturze danych
Drzewo AVL w strukturze danych odnosi się do drzewa Adelsona, Velskiego i Landisa. To jest ulepszona wersja drzewa wyszukiwania binarnego. Posiada wszystkie funkcje z drzewa wyszukiwania binarnego, ale różni się tylko tym, że zachowuje różnicę między wysokością lewego sub-drzewa i prawego sub-drzewa, a także zapewnia, że jego wartość wynosi <= 1 w drzewie, jest to znane jako Balance Czynnik.
Balance Factor = height(left-subtree) − height(right-subtree)
Na przykład: Rozważ następujące drzewa

W powyższym przykładzie wysokość prawego sub-drzewa = 2, a lewa = 3, a więc BF = 2, czyli <= 1, dlatego drzewo uważa się za zrównoważone.
Dlaczego potrzebujemy drzewa AVL w DS?
Podczas pracy z drzewem wyszukiwania binarnego natrafiamy na scenariusz, w którym elementy są posortowane. W takich przypadkach wszystkie elementy tablicy są umieszczone po jednej stronie korzenia, co prowadzi do zwiększenia złożoności czasowej wyszukiwania elementu w tablicy, a złożoność staje się - O (n), czyli najgorszy przypadek złożoności drzewa . Aby rozwiązać takie problemy i skrócić czas wyszukiwania, drzewa AVL zostały wynalezione przez Adelsona, Velskiego i Landisa.
Przykład:

Na powyższym rysunku wysokość lewego poddrzewa = 3 była jak
Wysokość prawego poddrzewa = 0
Zatem współczynnik równowagi = 3-0 = 3. Zatem wyszukiwanie elementu w takim drzewie ma złożoność O (n), która jest podobna do wyszukiwania liniowego. Aby uniknąć tego skomplikowanego wyszukiwania, wprowadzono drzewo AVL, w którym musi znajdować się każdy węzeł drzewa
współczynnik równowagi <= 1, w przeciwnym razie należy wykonać różne techniki rotacji w celu zrównoważenia takiego drzewa.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Rodzaje rotacji
Gdy współczynnik równowagi dla drzewa nie spełnia warunku <= 1, należy wykonać na nim obroty, aby zamienić je w drzewo zrównoważone.
Istnieją 4 rodzaje rotacji:
1. Obrót w lewo: jeśli dodanie węzła po prawej stronie drzewa powoduje, że staje się on niezrównoważony, wówczas w takim przypadku należy wykonać obrót w lewo.
2. Obrót w prawo: jeśli dodanie węzła po lewej stronie drzewa powoduje, że węzeł jest niezrównoważony, należy wykonać obrót w prawo. Innymi słowy, gdy liczba węzłów rośnie po lewej stronie, pojawia się potrzeba przesunięcia elementów na prawą stronę, aby ją zrównoważyć, dlatego mówi się, że jest to prawy obrót.
3. Obrót w lewo-prawo: Ten rodzaj obrotu jest kombinacją dwóch opisanych powyżej obrótów. Ten typ obrotu występuje, gdy jeden element jest dodawany do prawego poddrzewa lewego drzewa.
W takim przypadku najpierw wykonaj obrót w lewo w poddrzewie, a następnie obrót w prawo lewego drzewa.
4. Obrót w prawo-lewo: Ten typ obrotu składa się również z sekwencji powyżej 2 obrotów. Ten typ obrotu jest potrzebny, gdy element jest dodawany po lewej stronie prawego poddrzewa, a drzewo staje się niezrównoważone. W takim przypadku najpierw wykonujemy obrót w prawo w prawym poddrzewie, a następnie obrót w lewo na prawym drzewie.
Operacje na drzewie AVL w DS
Poniżej 3 operacji, które można wykonać na drzewie AVL: -
1. Wyszukaj
Ta operacja jest podobna do wyszukiwania w drzewie wyszukiwania binarnego. Wykonane kroki są następujące:
- Przeczytaj element dostarczony przez użytkownika, powiedz x.
- Porównaj element z katalogu głównego, jeśli jest taki sam, to wyjdź, w przeciwnym razie przejdź do następnego kroku.
- Jeśli x
W przeciwnym razie przejdź do odpowiedniego dziecka i porównaj ponownie.
Postępuj zgodnie z procesami B i C, aż znajdziesz element i wyjdź.
Ten proces ma złożoność O (log n).
Przykład:
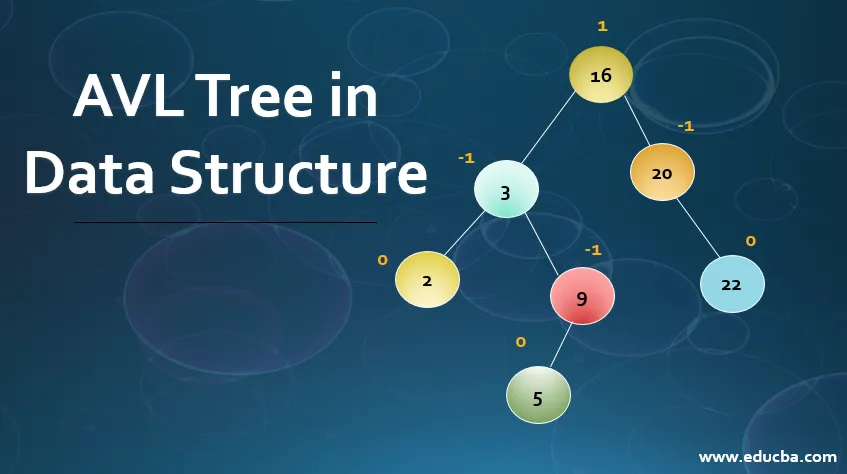
 | Rozważ to drzewo, w którym musimy przeprowadzić wyszukiwanie wartości węzła 9. Najpierw pozwól x = 9, wartość root (12)> x następnie wartość musi znajdować się w lewym poddrzewie elementu root. |
 | Teraz x jest porównywany z wartością węzła 3 x> 3 musimy zatem przejść do właściwego poddrzewa. |
 | Teraz x jest porównywane z węzłem (9), gdzie 9 == 9 zwraca true. W ten sposób wyszukiwanie elementów kończy się w drzewie. |
2. Wprowadzenie
Podczas wstawiania elementu do drzewa AVL musimy znaleźć lokalizację konkretnego elementu, który należy wstawić, a następnie element jest dołączany tak samo, jak wstawianie w BST, ale po tym jest sprawdzane, czy drzewo jest nadal zrównoważone, czy nie tzn. współczynnik równowagi węzła wynosi <= 1. Poszczególne obroty są wykonywane zgodnie z wymaganiami.
Złożoność wynosi O (log n).
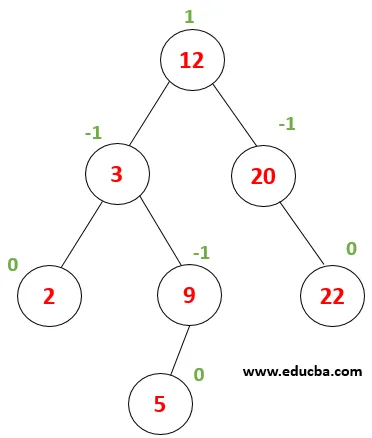
Przykład: rozważ poniższe drzewo,
 | Każdy węzeł ma współczynnik równowagi równy 0, -1 lub 1, więc drzewo jest zrównoważone. Teraz pozwala, co się dzieje, gdy wstawiany jest węzeł o wartości 1. Pierwsze drzewo przechodzi, aby znaleźć lokalizację, w której należy go wstawić… 1 <2 jest więc zapisywane jako lewe dziecko węzła (2). |
 | Po wstawieniu węzeł (9) staje się niezrównoważony ze współczynnikiem równowagi = 2. Teraz podlega rotacji w prawo. |
 | Drzewo staje się wyważone po obrocie w prawo, dzięki czemu operacja wstawiania zakończyła się pomyślnie. |
3. Usunięcie
Usunięcie elementu z drzewa AVL obejmuje również wyszukiwanie elementu w drzewie, a następnie usunięcie go. Operacja wyszukiwania jest taka sama, jak BST, a po znalezieniu elementu do usunięcia element jest usuwany z drzewa, a elementy są dostosowywane, aby ponownie uzyskać BST. Po sprawdzeniu, czy elementy te mają współczynnik równowagi 0, -1 lub 1, a zatem wykonywane są odpowiednie obroty w celu zrównoważenia.
Złożoność, jeśli O (log n).
 | Rozważ dane drzewo, którego wszystkie mają współczynnik równowagi 0, -1 lub 1. Teraz usuńmy węzeł o wartości 16. Pierwsze drzewo jest przeszukiwane w celu znalezienia węzła o wartości 16 takiej samej jak algorytm wyszukiwania. |
 | Węzeł 16 zostanie zastąpiony wewnętrznym poprzednikiem tego węzła, który jest największym elementem z lewego poddrzewa, tj. 12 Drzewo zostało niezrównoważone, dlatego LL - rotacja musi zostać wykonana. |
 | Teraz każdy węzeł został zrównoważony. |
Wniosek - drzewo AVL w strukturze danych
Drzewo AVL jest potomkiem drzewa wyszukiwania binarnego, ale przezwycięża swoją wadę polegającą na zwiększaniu złożoności w przypadku sortowania elementów. Monitoruje współczynnik równowagi drzewa na 0 lub 1 lub -1. W przypadku niezrównoważenia drzewa wykonywane są odpowiednie techniki rotacji w celu zrównoważenia drzewa.
Polecane artykuły
Jest to przewodnik po drzewie AVL w strukturze danych. Tutaj omawiamy wprowadzenie, operacje na drzewie AVL w DS i typy rotacji. Możesz także przejrzeć nasze inne powiązane artykuły, aby dowiedzieć się więcej -
- jQuery Elements
- Czym jest Data Science
- Rodzaje drzew w strukturze danych
- Typy danych C #