Wzór zwrotu portfela (spis treści)
- Formuła
- Przykłady
- Kalkulator
Co to jest formuła zwrotu portfela?
Zwrot z portfela to zwrot uzyskany z zysku lub straty zrealizowanej przez portfel inwestycyjny, który składa się z kilku rodzajów inwestycji. Portfele mają na celu zapewnienie zwrotu na podstawie wstępnie określonej strategii inwestycyjnej, aby zrealizować cel inwestycyjny, a także tolerancji ryzyka dla rodzaju inwestorów, których dotyczy portfel.
Oczekiwany zwrot z portfela:
Oczekiwany zwrot z portfela to suma każdego produktu oczekiwanego zwrotu z poszczególnych aktywów wraz z powiązaną wagą.
R p = ∑ (W i * R i )
Gdzie i = 1, 2, 3, …… .n
- W i : Definiuje powiązaną wagę z aktywem i
- R i : Jest to zwrot z aktywów
Waga przypisana do składnika aktywów = wartość rynkowa aktywów / wartość rynkowa portfela
Odchylenie portfela:
Wariancja zwrotu z portfela jest funkcją poszczególnych aktywów i kowariancji między nimi. Jeśli mamy dwa aktywa, A i B,
Portfolio Variance = W A 2 *σ 2 *R A + W B 2 *σ 2 *R B + 2*W A *W B *Cov(R A, R B )
Wariancja portfela jest miarą ryzyka, więcej wariancji, większe ryzyko. Zazwyczaj inwestor próbuje zmniejszyć ryzyko, wybierając ujemne aktywa kowariancji, takie jak akcje i obligacje.
Odchylenie standardów portfela:
Jest to po prostu pierwiastek kwadratowy wariancji portfela.
SD = √ (W A 2 * σ 2 * R A + W B 2 * σ 2 * R B + 2 * W A * W B * Cov(R A, R B ))
I jest to miara ryzyka portfela.
Przykłady formuły zwrotu portfela (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie zwrotu z portfela.
Możesz pobrać ten szablon Excel Formula Formula Excel - Portfolio Formula Formula ExcelWzór zwrotu portfela - przykład nr 1
Jeśli weźmiemy przykład, inwestujesz 60 000 USD w aktywa 1, które przyniosło 20% zwrotów, a 40 000 USD inwestujesz w aktywa 2, które generują 12% zysków. Ich odpowiednia waga dystrybucji wynosi 60% i 40%. Oblicz zwrot z portfela.
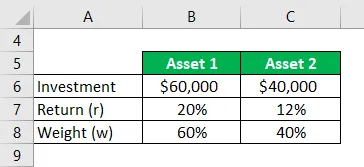
Rozwiązanie:
Zwrot portfela jest obliczany przy użyciu poniższej formuły
R p = ∑ (w i * r i )
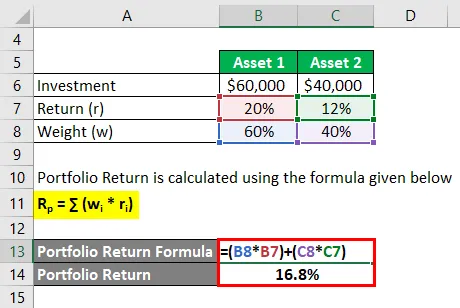
- Zwrot z portfela = (60% * 20%) + (40% * 12%)
- Zwrot z portfela = 16, 8%
Wzór zwrotu portfela - przykład 2
Zastanów się, czy inwestor planuje zainwestować w trzy akcje, które są Akcją A, a jej oczekiwany zwrot w wysokości 18% i wartość zainwestowanej kwoty wynosi 20 000 USD, a ona jest również zainteresowana własną Akcją w wysokości 25 000 B $, która ma spodziewany zwrot w wysokości 12%. Podczas gdy spodziewany zwrot akcji C wynosi 30 000 USD w wysokości 10%. Czy teraz jest zainteresowana obliczeniem całkowitego zwrotu, jaki uzyskałaby ze swojego portfela?
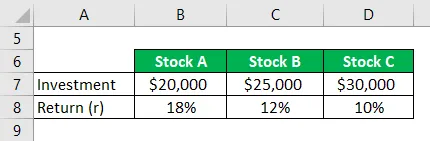
Rozwiązanie:
Waga każdej inwestycji jest obliczana jako
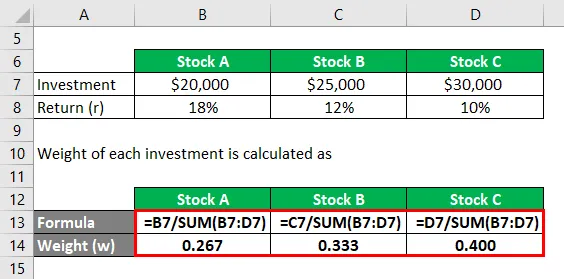
- Akcje A = 20 000 USD / (20 000 USD + 25 000 USD + 30 000 USD) = 0, 267
- Zapas B = 25 000 USD / (20 000 USD + 25 000 USD + 30 000 USD) = 0, 333
- W Stock C = 30 000 USD / (20 000 USD + 25 000 USD + 30 000 USD) = 0, 400
Zwrot portfela jest obliczany przy użyciu poniższej formuły
R p = ∑ (w i * r i )
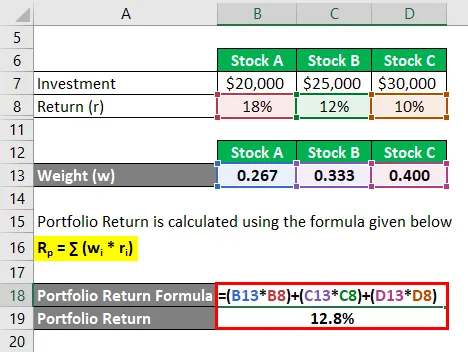
- Zwrot z portfela = (0, 267 * 18%) + (0, 333 * 12%) + (0, 400 * 10%)
- Zwrot z portfela = 12, 8%
Tak więc ogólny wynik oczekiwanego zwrotu wynosi 12, 8%
Wzór zwrotu portfela - przykład 3
Jeśli zainwestujesz 600 USD w IBM i 400 USD w Merck na miesiąc. A jeśli zdałeś sobie sprawę, że zwrot wynosi 2, 5% na IBM i 1, 5% na Merck w ciągu miesiąca, obliczyć zwrot z portfela?
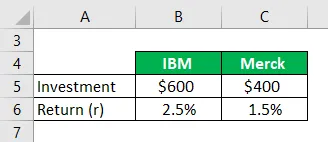
Rozwiązanie:
Waga każdej inwestycji jest obliczana jako
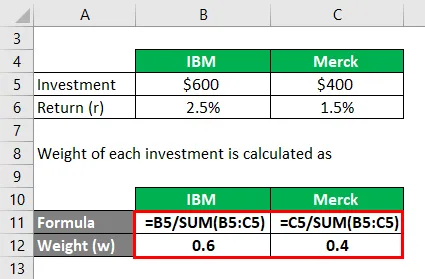
- W IBM = 600 USD / (600 USD + 400 USD) = 0, 6
- W Merck = 400 USD / (600 USD + 400 USD) = 0, 4
Zwrot portfela jest obliczany przy użyciu poniższej formuły
R p = ∑ (w i * r i )
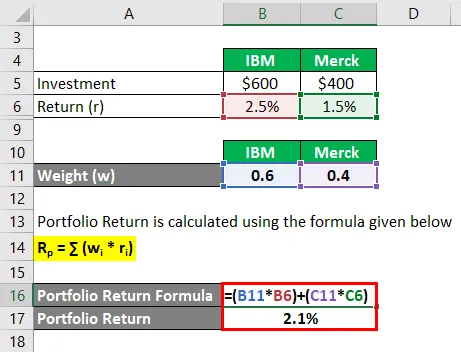
- Zwrot z portfela = (0, 6 * 2, 5%) + (0, 4 * 1, 5%)
- Zwrot z portfela = 2, 1%
Wyjaśnienie
Zwrot z portfela jest miarą zwrotu poszczególnych aktywów. Jednak zwrot z portfela jest średnią ważoną zwrotów z jego aktywów składowych.
Oto pewien predefiniowany zestaw procedur do obliczania formuły oczekiwanego zwrotu dla portfela.
Krok 1: Na początku naszą intuicją jest określenie zwrotu uzyskanego z każdej inwestycji portfela oznaczonej jako r.
Krok 2 : Następnie należy ustalić wagę każdego składnika aktywów w portfelu na podstawie bieżącej rynkowej ceny handlowej tego składnika. który jest oznaczony przez w.
Krok 3 : Wreszcie oczekiwany zwrot z portfela jest obliczany na podstawie sumy iloczynu wagi każdej inwestycji w portfelu, a zwroty z każdej odpowiedniej inwestycji są otrzymywane w następujący sposób:
Oczekiwany zwrot z portfela = ∑ (w i * r i )
Trafność i zastosowania formuły zwrotu portfela
Pojęcie równania oczekiwanego zwrotu z portfela jest obowiązkowe, aby zrozumieć, co pomaga przewidywać zysk lub stratę inwestora z inwestycji. Formuła oczekiwanego zwrotu to formuła, którą inwestor może zdecydować, czy może dalej inwestować w składnik aktywów, aby uzyskać dane prawdopodobne zwroty.
Inwestor musi rozważyć znacznie więcej na temat wagi aktywów w portfelu i ewentualnego wymaganego ulepszenia.
Inwestor klasyfikuje składnik aktywów na podstawie formuły oczekiwanego zwrotu, uwzględnia w portfelu i dokonuje w nim inwestycji. Im wyższy oczekiwany zwrot, tym lepiej.
Celem utworzenia portfela jest zmniejszenie ogólnego ryzyka i zmienności inwestycji oraz ciągłe dążenie do uzyskania lepszej dodatniej stopy zwrotu. Analityk i badacz analizują dane historyczne i próbują przewidzieć, które akcje mają znaleźć się w portfelu. Ujemna kowariancja włączonych aktywów zmniejsza ogólną zmienność portfela i zwiększa zwroty. A dodatnia kowariancja wskazuje, że dwa aktywa poruszają się sekwencyjnie, podczas gdy w ujemnej kowariancji dwa aktywa poruszają się w przeciwnych kierunkach. Zróżnicowanego ryzyka nie można zminimalizować po dodaniu 25 różnych akcji w portfelu. Współczynnik korelacji jest głównie wykorzystywany do określania relacji między dwoma aktywami i mierzenia ich siły.
Kalkulator formuły zwrotu portfela
Możesz użyć następującego kalkulatora zwrotu portfela
| w 1 | |
| r 1 | |
| w 2 | |
| r 2 | |
| R p | |
| R p = | (w 1 xr 1 ) + (w 2 xr 2 ) |
| = | (0 x 0) + (0 x 0) = 0 |
Polecane artykuły
Jest to przewodnik po formule zwrotu portfela. Tutaj omawiamy sposób obliczania zwrotu z portfela wraz z praktycznymi przykładami. Oferujemy również kalkulator zwrotu portfela z szablonem Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Co to jest formuła dochodu rezydualnego?
- Formuła zwrotu z okresu posiadania
- Przykłady wzoru analizy wariancji
- Jak obliczyć współczynnik determinacji?