
Wprowadzenie do algorytmu DFS
DFS jest znany jako Algorytm pierwszego wyszukiwania głębokości, który zapewnia kroki do przejścia przez każdy węzeł wykresu bez powtarzania żadnego węzła. Ten algorytm jest taki sam jak w przypadku głębokości pierwszego przejścia dla drzewa, ale różni się utrzymywaniem wartości logicznej w celu sprawdzenia, czy węzeł był już odwiedzany, czy nie. Jest to ważne dla przechodzenia przez wykres, ponieważ cykle istnieją również na wykresie. W tym algorytmie utrzymywany jest stos do przechowywania zawieszonych węzłów podczas przechodzenia. Jest tak nazwany, ponieważ najpierw podróżujemy na głębokość każdego sąsiedniego węzła, a następnie kontynuujemy przemierzanie innego sąsiedniego węzła.
Wyjaśnij algorytm DFS
Algorytm ten jest sprzeczny z algorytmem BFS, w którym odwiedzane są wszystkie sąsiednie węzły, a następnie sąsiedzi sąsiednich węzłów. Zaczyna eksplorować wykres od jednego węzła i bada jego głębokość przed cofnięciem. Algorytm uwzględnia dwie rzeczy:
- Zwiedzanie wierzchołka: Wybór wierzchołka lub węzła wykresu do przejścia.
- Eksploracja wierzchołka: Przechodzenie przez wszystkie węzły sąsiadujące z tym wierzchołkiem.
Pseudo-kod dla pierwszego wyszukiwania głębokości :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Dla systemu plików DFS istnieje również przejście liniowe, które można zaimplementować na 3 sposoby:
- Przed Sprzedaż
- W celu
- Po zamówieniu
Odwrotna kolejność jest bardzo użytecznym sposobem na przechodzenie i wykorzystywana w sortowaniu topologicznym, a także w różnych analizach. Utrzymywany jest również stos do przechowywania węzłów, których eksploracja wciąż trwa.
Traverse wykresu w DFS
W systemie plików DFS należy wykonać poniższe kroki, aby przejść przez wykres. Na przykład, dany wykres, zacznijmy przemierzanie od 1:
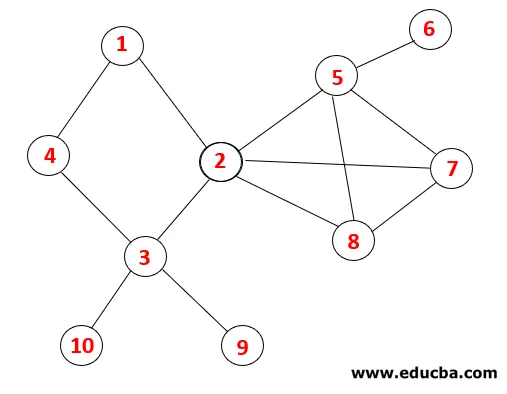
| Stos | Sekwencja ruchu | Spanning Tree |
| 1 |  |
|
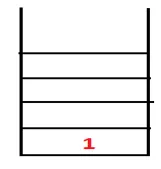 | 1, 4 |  |
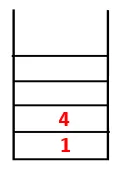 | 1, 4, 3 |  |
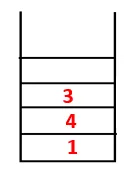 | 1, 4, 3, 10 | 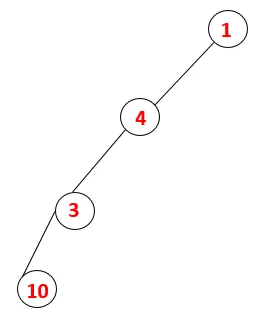 |
 | 1, 4, 3, 10, 9 | 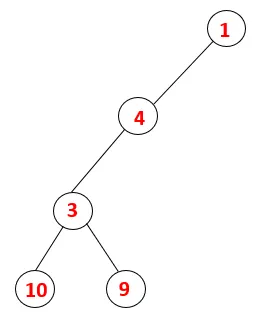 |
 | 1, 4, 3, 10, 9, 2 | 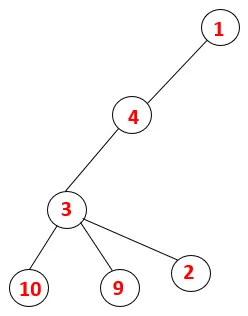 |
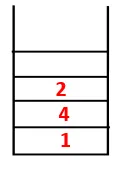 | 1, 4, 3, 10, 9, 2, 8 |  |
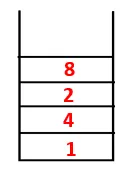 | 1, 4, 3, 10, 9, 2, 8, 7 | 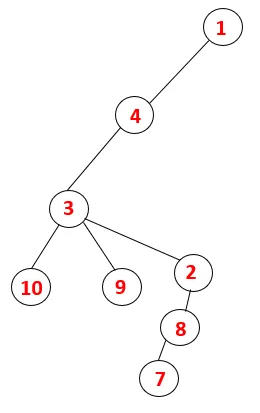 |
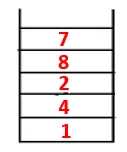 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
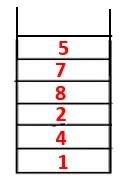 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 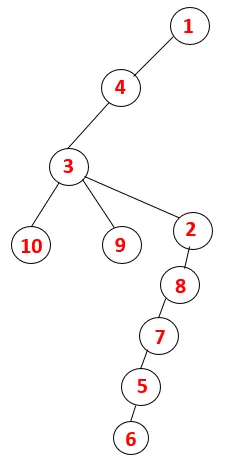 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 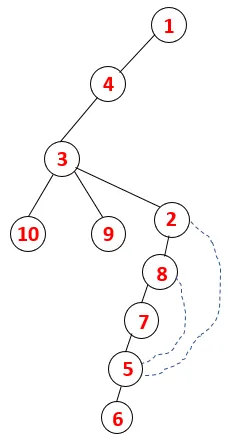 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
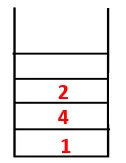 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 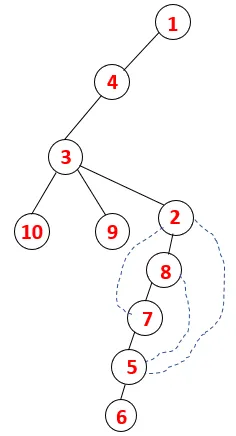 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 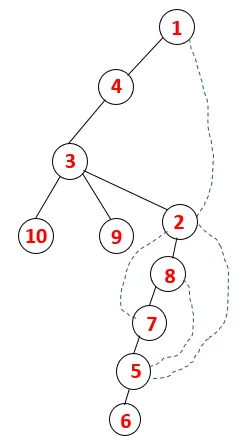 |
Objaśnienie do algorytmu DFS
Poniżej znajdują się kroki do algorytmu DFS z zaletami i wadami:
Krok 1: Węzeł 1 jest odwiedzany i dodawany do sekwencji oraz drzewa opinającego.
Krok 2: Eksplorowane są sąsiednie węzły 1, czyli 4, dlatego 1 jest wypychany na stos, a 4 jest wpychany do sekwencji, a także do drzewa opinającego.
Krok 3: Jeden z sąsiednich węzłów 4 zostaje zbadany, a zatem 4 zostaje zepchnięty na stos, a 3 wchodzi do sekwencji i drzewa rozpinającego.
Krok 4: Sąsiadujące węzły 3 są badane przez wepchnięcie go na stos i 10 wchodzi do sekwencji. Ponieważ nie ma sąsiadującego węzła z 10, 3 jest wyskakujące ze stosu.
Krok 5: Kolejny sąsiadujący węzeł 3 zostaje zbadany, a 3 zostaje wepchnięty na stos, a 9 odwiedzonych. Żaden sąsiadujący węzeł 9 nie jest wyskakujący, a ostatni sąsiadujący węzeł 3, tj. 2, jest odwiedzany.
Podobny proces jest wykonywany dla wszystkich węzłów, aż stos stanie się pusty, co wskazuje na warunek zatrzymania dla algorytmu przechodzenia. - -> kropkowane linie w drzewie opinającym odnoszą się do tylnych krawędzi obecnych na wykresie.
W ten sposób wszystkie węzły na wykresie przechodzą bez powtarzania żadnego z węzłów.
Zalety i wady
- Zalety: Wymagania dotyczące pamięci dla tego algorytmu są bardzo mniejsze. Mniejsza złożoność przestrzeni i czasu niż BFS.
- Wady: Rozwiązanie nie jest gwarantowane Aplikacje. Sortowanie topologiczne. Znajdowanie mostów wykresu.
Przykład implementacji algorytmu DFS
Poniżej znajduje się przykład implementacji algorytmu DFS:
Kod:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Wynik:
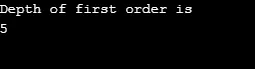
Objaśnienia do powyższego programu: Stworzyliśmy wykres mający 5 wierzchołków (0, 1, 2, 3, 4) i wykorzystaliśmy tablicę odwiedzin do śledzenia wszystkich odwiedzanych wierzchołków. Następnie dla każdego węzła, którego sąsiadujące węzły istnieją, ten sam algorytm powtarza się, aż wszystkie węzły zostaną odwiedzone. Następnie algorytm wraca do wywoływania wierzchołka i wyskakuje ze stosu.
Wniosek
Zapotrzebowanie na pamięć tego wykresu jest mniejsze w porównaniu do BFS, ponieważ do utrzymania wymagany jest tylko jeden stos. W wyniku tego generowane jest drzewo rozpinające DFS i sekwencja przechodzenia, ale nie jest stała. Możliwa jest wielokrotna sekwencja przejścia w zależności od wybranego wierzchołka początkowego i wierzchołka eksploracji.
Polecane artykuły
Jest to przewodnik po algorytmie DFS. Tutaj omawiamy wyjaśnienia krok po kroku, przeglądaj wykres w formacie tabeli z zaletami i wadami. Możesz również przejrzeć nasze inne powiązane artykuły, aby dowiedzieć się więcej -
- Co to jest HDFS?
- Algorytmy głębokiego uczenia się
- Polecenia HDFS
- Algorytm SHA