
Wprowadzenie do przykładów odchyleń standardowych
Istnieje wiele przykładów odchyleń standardowych. Odchylenie standardowe jest miarą rozproszenia zestawu danych, tj. Stopnia rozłożenia liczb. Jest to przydatne do porównywania różnych zestawów danych, które mogą mieć tę samą średnią, ale inny zakres. Poniższy inny przykład odchylenia standardowego daje zrozumienie na temat najczęstszych rodzajów sytuacji, w których oblicza się odchylenie standardowe i jak można obliczyć to samo
Przykłady odchylenia standardowego
Poniżej znajdują się przykłady odchylenia standardowego
Odchylenie standardowe - przykład nr 1
Akcje Spółki Z sprzedają się za 50 USD za akcję i te same oferty po wypłatach na następny rok:
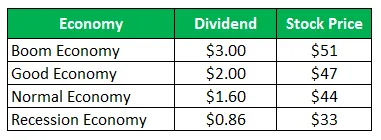
Oblicz odchylenie standardowe, gdy wszystkie cztery scenariusze są równie prawdopodobne.
Rozwiązanie:
Obliczenia zwrotu z okresu posiadania (HPR) są następujące:
Formuła HPR
HPR = ((wartość końcowa okresu - wartość początkowa) + dochód) / wartość początkowa) * 100
Dla Boom Economy
- HPR (wysięgnik) = ((51-50) + 3) / 50 = 8, 00%
- HPR (dobra) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normalny) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recesja) = ((33-50) + 0, 86) / 50 = -32, 28%
Obliczanie oczekiwanego zwrotu
Ponieważ wszystkie scenariusze są jednakowo prawdopodobne, więc prawdopodobieństwo wszystkich wyniesie ¼
Formuła oczekiwanego zwrotu
Oczekiwany zwrot = (Prawdopodobieństwo boomu * Powrót z boomu) + (Prawdopodobieństwo dobra * Return from Good) + (Prawdopodobieństwo normalnego * Return from Normal) + (Prawdopodobieństwo recesji * Return from Recession)
- Oczekiwany zwrot = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Oczekiwany zwrot = -8, 77%
Obliczanie odchylenia standardowego
Formuła wariancji
Wariancja = (Prawdopodobieństwo boomu * (Return from Boom - Total Oczekiwany zwrot) 2) + (Prawdopodobieństwo Good * (Return from Good - Całkowity oczekiwany zwrot) 2) + (Prawdopodobieństwo Normal * (Return from Normal - Total Oczekiwany zwrot) 2 ) + (prawdopodobieństwo recesji * (zwrot z recesji - całkowity oczekiwany zwrot) 2)
- Wariancja = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Wariancja = 219, 95
Formuła odchylenia standardowego
Odchylenie standardowe będzie Pierwiastkiem Różnicowym
Odchylenie standardowe = √ Wariant
- Odchylenie standardowe = 9 219, 95
- Odchylenie standardowe = 14, 83%
Przykład odchylenia standardowego - 2
Odchylenie standardowe w przypadku dwóch spółek w portfelu
Akcje zwykłe Spółki A sprzedają się za 28 USD za akcję i te same oferty po wypłatach na następny rok

Akcje zwykłe spółki B sprzedają się za 93 USD za akcję i te same oferty po wypłatach na następny rok:

(a) Oblicz odchylenie standardowe dla Firmy A.
(b) Oblicz odchylenie standardowe dla Firmy B
(c) Oblicz odchylenie standardowe portfela, jeśli połowa inwestycji jest dokonana przez firmę A, a druga połowa w firmie B
Rozwiązanie:
Dla firmy A.
Obliczenia zwrotu z okresu posiadania (HPR)
Formuła HPR
HPR = ((wartość końcowa okresu - wartość początkowa) + dochód) / wartość początkowa) * 100
- HPR (wysięgnik) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normalny) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recesja) = ((38–28) + 5) / 28 = 53, 57%
Obliczanie oczekiwanego zwrotu firmy A
Formuła oczekiwanego zwrotu
Oczekiwany zwrot = (Prawdopodobieństwo boomu * Powrót z boomu) + (Prawdopodobieństwo normalnego * Return from Normal) + (Prawdopodobieństwo recesji * Return from Recession)
- Oczekiwany zwrot = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Oczekiwany zwrot = 3, 84%
Obliczanie odchylenia standardowego Firma A
Formuła wariancji
Wariancja = (prawdopodobieństwo boomu * (zwrot z boomu - całkowity oczekiwany zwrot) 2) + (prawdopodobieństwo normalnego * (powrót z normalnego - całkowity oczekiwany zwrot) 2 ) + (prawdopodobieństwo recesji * (powrót z recesji - całkowity oczekiwany zwrot) 2)
- Wariancja = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Wariancja = 895, 15
Formuła odchylenia standardowego
Odchylenie standardowe będzie Pierwiastkiem Różnicowym
Odchylenie standardowe = √ Wariant
- Odchylenie standardowe = 95 895, 15
- Odchylenie standardowe = 29, 92%
Dla firmy B
Obliczenia zwrotu z okresu posiadania (HPR)
Formuła HPR
HPR = ((wartość końcowa okresu - wartość początkowa) + dochód) / wartość początkowa) * 100
HPR (wysięgnik) = ((200-93) +7) / 93 = 122, 58%
HPR (normalny) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recesja) = ((4-93) +2) / 93 = -93, 55%
Obliczanie oczekiwanego zwrotu
Formuła oczekiwanego zwrotu
Oczekiwany zwrot = (Prawdopodobieństwo boomu * Powrót z boomu) + (Prawdopodobieństwo normalnego * Return from Normal) + (Prawdopodobieństwo recesji * Return from Recession)
- Oczekiwany zwrot = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Oczekiwany zwrot = 43, 04%
Obliczanie odchylenia standardowego
Formuła wariancji
Wariancja = (prawdopodobieństwo boomu * (zwrot z boomu - całkowity oczekiwany zwrot) 2) + (prawdopodobieństwo normalnego * (powrót z normalnego - całkowity oczekiwany zwrot) 2 ) + (prawdopodobieństwo recesji * (powrót z recesji - całkowity oczekiwany zwrot) 2)
- Wariancja = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Wariancja = 6783, 65
Formuła odchylenia standardowego
Odchylenie standardowe będzie Pierwiastkiem Różnicowym
Odchylenie standardowe = √ Wariant
- Odchylenie standardowe = 786783, 65
- Odchylenie standardowe = 82, 36%
Obliczanie oczekiwanego zwrotu i odchylenia standardowego portfela w połowie zainwestowanego w firmie A i w połowie w firmie B.
Odchylenie standardowe firmy A = 29, 92%
Odchylenie standardowe firmy B = 82, 36%
Waga firmy A = 0, 50
Waga firmy B = 0, 50
Formuła odchylenia standardowego portfela
Odchylenie standardowe portfela = (waga firmy A * oczekiwany zwrot firmy A) + ((waga firmy B * oczekiwany zwrot firmy B)
- Odchylenie standardowe portfela = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Odchylenie standardowe portfela = 56, 14%
Analiza
Odchylenie standardowe portfela jest niższe niż dla poszczególnych akcji, ponieważ zapasy są zróżnicowane pod kątem różnych akcji. Dywersyfikacja prowadzi do zmniejszenia ryzyka, chyba że istnieje idealna korelacja między zwrotami z inwestycji portfelowych.
Wniosek - przykłady odchyleń standardowych
Odchylenie standardowe mierzy rozrzut zbioru danych w stosunku do jego średniej. Jest obliczany jako pierwiastek kwadratowy wariancji. Im większe jest standardowe odchylenie zabezpieczenia, tym większa będzie wariancja między każdą ceną a średnią, co pokazuje, że przedział cenowy jest duży. Wyżej wymienione przykłady są niektórymi przykładami odchylenia standardowego na różne sposoby. Istnieje również wiele innych przykładów, które pokazują, że odchylenie standardowe można obliczyć przy użyciu innych danych.
Polecane artykuły
Jest to przewodnik po standardowych przykładach odchyleń. Tutaj omawiamy różne przykłady odchylenia standardowego wraz ze szczegółowym wyjaśnieniem . Możesz także zapoznać się z następującymi artykułami, aby dowiedzieć się więcej -
- Przykład kosztów stałych
- Przykład zmiennego kosztu
- Przykład badań ilościowych
- Przykłady konkurencji monopolistycznej