Excel NORMSINV (spis treści)
- Wprowadzenie do programu Excel NORMSINV
- Jak korzystać z formuły NORMSINV w programie Excel?
Wprowadzenie do programu Excel NORMSINV
Funkcja odwrotności normalnego skumulowanego rozkładu w programie Excel jest ważnym narzędziem, które zwraca odwrotny normalny rozkład skumulowany dla danej wartości prawdopodobieństwa, tj. Zwykle zwraca odwrotność standardowego normalnego skumulowanego rozkładu (który ma średnią zero i standardowe odchylenie jeden) Funkcja NORM.S.INV została po raz pierwszy wprowadzona w Microsoft Excel w wersji 2010, która jest zaktualizowaną wersją funkcji NORMSINV w programie Excel 2013 i najnowszą wersją. Funkcja NORMSINV jest wykorzystywana głównie w analizie zobowiązań i analiz finansowych.
Składnia Excel NORMSINV

Argument:
Prawdopodobieństwo - które jest niczym innym jak prawdopodobieństwem odpowiada rozkładowi normalnemu.
Jak korzystać z formuły NORMSINV w programie Excel?
W Microsoft Excel wbudowana funkcja NORMSINV jest podzielona na funkcje statystyczne, które pokazano na poniższym zrzucie ekranu (gdzie obliczy odwrotność normalnego skumulowanego rozkładu dla danego prawdopodobieństwa).
- Przejdź do menu Formuły.
- Kliknij Więcej funkcji, jak pokazano na zrzucie ekranu poniżej.

- Wybierz kategorię statystyczną, pod którą znajdziemy funkcję NORM.DIST, jak pokazano poniżej.
Przykład # 1 - Używanie NORM.DIST i NORMSINV
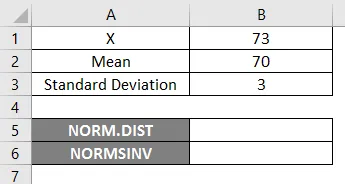
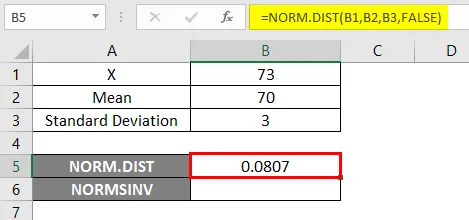
Aby skorzystać z funkcji NORM.DIST, zacznijmy od prostego przykładu, w którym musimy znaleźć oceny uczniów. Załóżmy, że mamy egzamin klasowy ze średnią oceną 70, tj. Mu = 70, a odchylenie standardowe klasy to 3 punkty, tj. Sigma = 3 tutaj musimy dowiedzieć się, jakie jest prawdopodobieństwo, że uczniowie otrzymają oceny 73 lub niższe, tj. P (X <= 73). Zobaczmy więc, jak znaleźć prawdopodobieństwo za pomocą funkcji NORM.DIST.
- X = 3
- Średnia = 70
- Odchylenie standardowe = 3
- Zastosuj funkcję NORM.DIST jak poniżej.
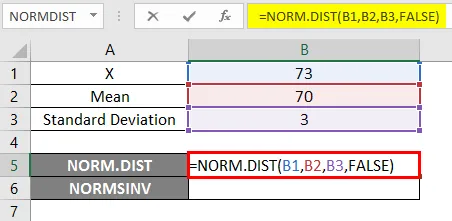
- Jeśli zastosujemy powyższą funkcję NORM.DIST, otrzymamy prawdopodobieństwo 0, 0807.
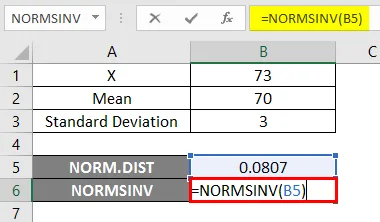
- Teraz zastosuj funkcję NORMSINV, aby znaleźć odwrotność normalnego skumulowanego rozkładu, jak pokazano poniżej.
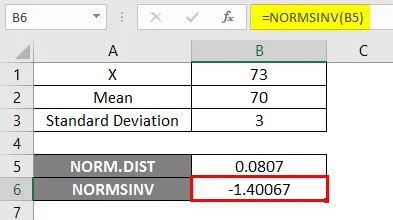
Wynik -
W poniższym wyniku widzimy, że otrzymaliśmy wartości ujemne -1.40067 dla danego prawdopodobieństwa, tj. Odwrotność normalnego rozkładu skumulowanego.
Przykład # 2 - Średnie i dokładne odchylenie standardowe
Zobaczmy kolejny przykład z danymi opartymi na krzywej, abyśmy mogli poznać średnią i dokładne odchylenie standardowe.
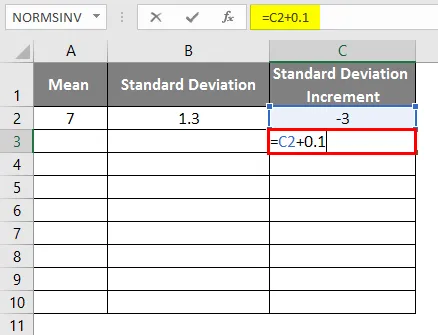
- Średnia = 7
- Odchylenie standardowe = 1, 3
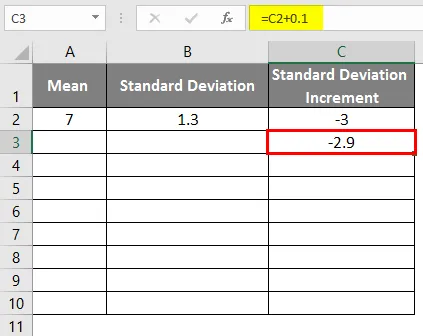
- Przyrost odchylenia standardowego jako -3

- Aby uzyskać krzywą dzwonową, musimy dodać 0, 1 do przyrostu odchylenia standardowego, gdzie dane są jak pokazano poniżej.
- Po zastosowaniu formuły wynik jest taki, jak pokazano poniżej.
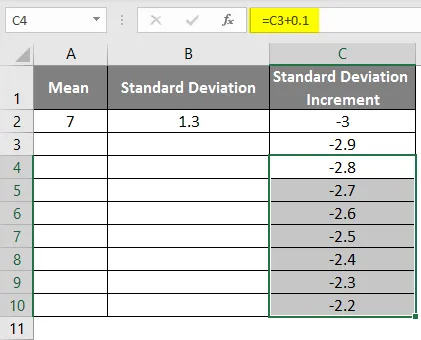
- Przeciągnij wartości, aby uzyskać więcej wartości, aż uzyskamy wartości dodatnie, aby uzyskać lewą krzywą.
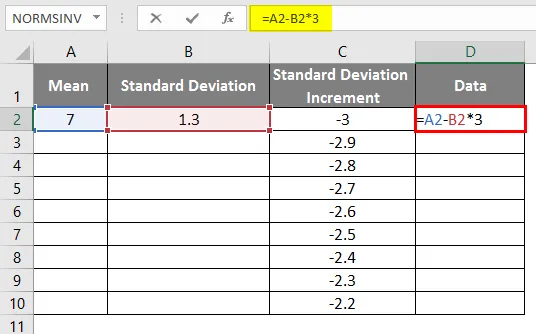
- Aby uzyskać właściwą krzywą, musimy zastosować formułę = średnie odchylenie standardowe * 3, aby uzyskać dokładne krzywe.
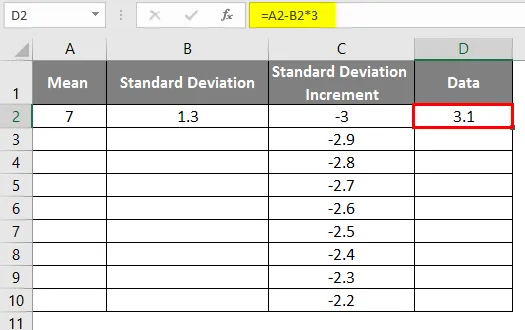
- Po użyciu formuły wynik pokazano poniżej.
- Jak w powyższych danych dla przyrostu odchylenia standardowego w celu uzyskania krzywej lewej, zwiększyliśmy wartości o 0, 1
- Ten sam scenariusz stosuje się, stosując wzór na = 3.1 + ODCHYLENIE STANDARDOWE / 10, aby uzyskać przyrost krzywej 0, 1
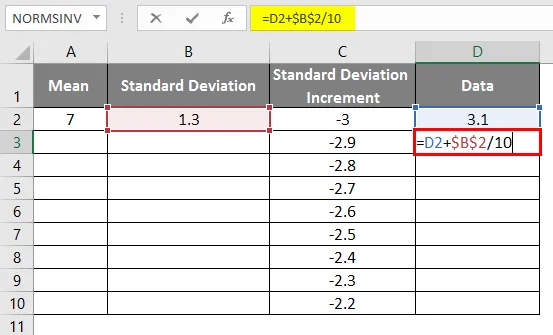
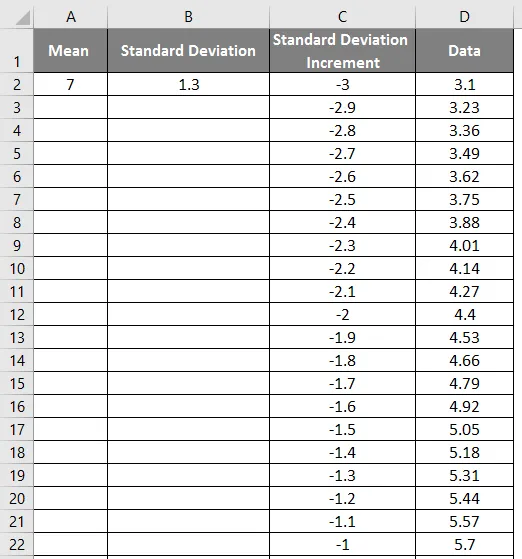
- Po użyciu formuły wynik pokazano poniżej.

- Przeciągnij wartości, aby uzyskać dokładny wynik pokazany na poniższym zrzucie ekranu.
- Teraz zastosuj funkcję rozkładu normalnego ze wzorem = NORM.DIST (wartość danych, średnia, odchylenie standardowe, fałsz).
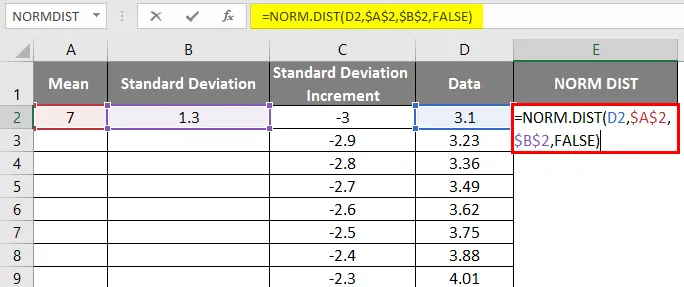
- Otrzymamy poniższy wynik w następujący sposób.
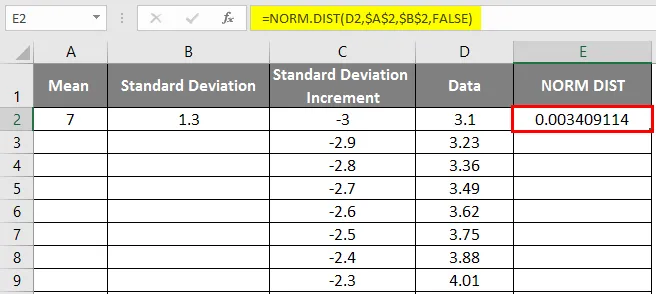
- Przeciągnij wartości, aby uzyskać dokładny wynik, który pokazano poniżej.
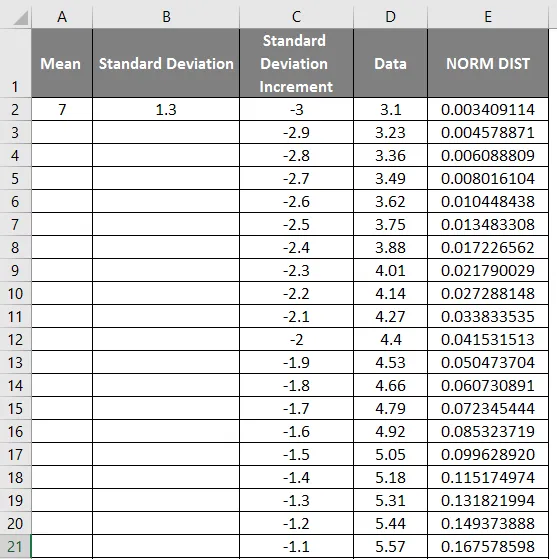
- Jak widać na powyższym zrzucie ekranu, obliczyliśmy rozkład NORMALNY na podstawie średniej i odchylenia standardowego. Zobaczmy teraz, co będzie odwrotnością rozkładu NORMALNEGO poprzez zastosowanie NORMSINV, co pokazano poniżej.
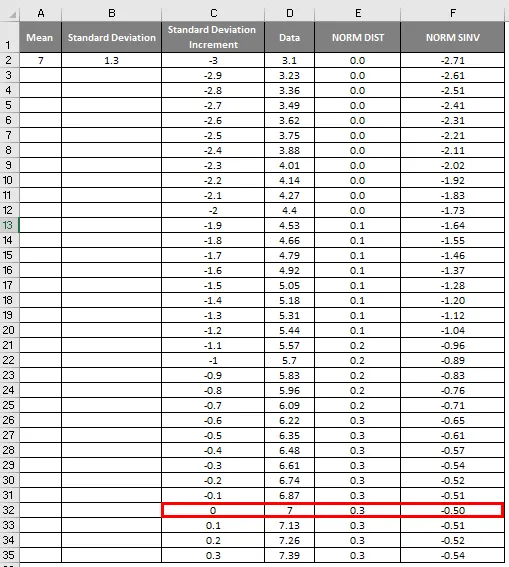
- Tutaj widzimy, że wartość zero (0) ma odchylenie standardowe równe 7.

Zastosowanie wykresu rozproszonego, aby zobaczyć, jak wygląda lewa i prawa krzywa.
- Najpierw wybierz dane i kolumnę Normalny.
- Przejdź do zakładki Wstaw i wybierz wykres rozproszony w następujący sposób.
- Otrzymamy poniższy wykres krzywej, jak pokazano poniżej.
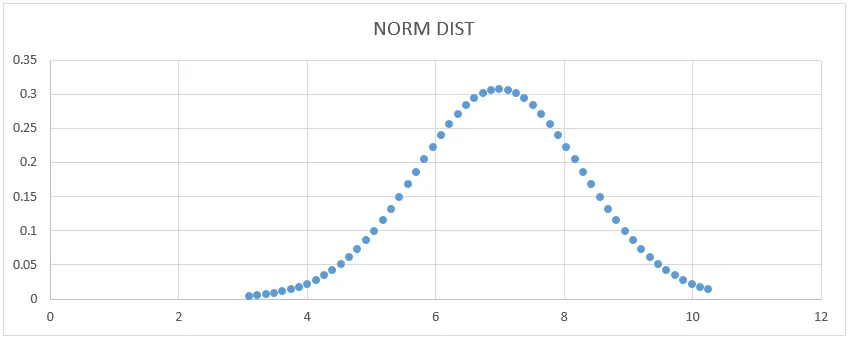
Tutaj widzimy, że Średnia wartość 7 ma kształt odchylenia standardowego, w którym możemy to pokazać, rysując linię prostą do jej przedstawienia.
- Średnia = 7
- 1 - Odchylenie standardowe wskazuje 68% danych.
- 2 - Odchylenie standardowe wskazuje 95% danych.
- 3 - Odchylenie standardowe wskazuje 99, 7% danych.
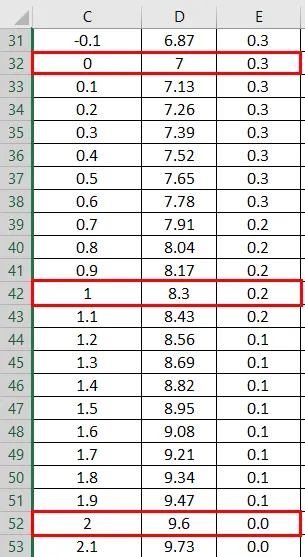
Wykres rozkładu normalnego:
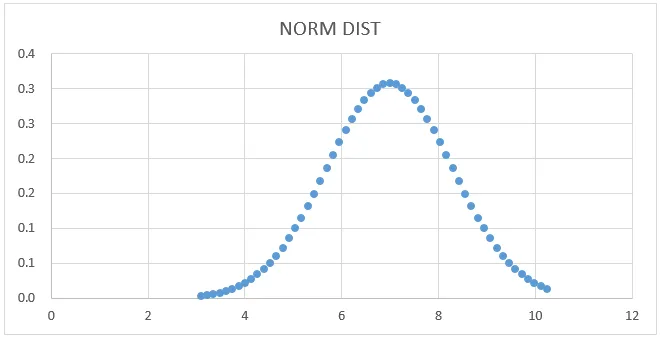
Wykres NORMSINV:
Teraz z powyższego rysunku wybierz kolumnę danych i NORM SINV, aby uzyskać poniższy wykres w następujący sposób.
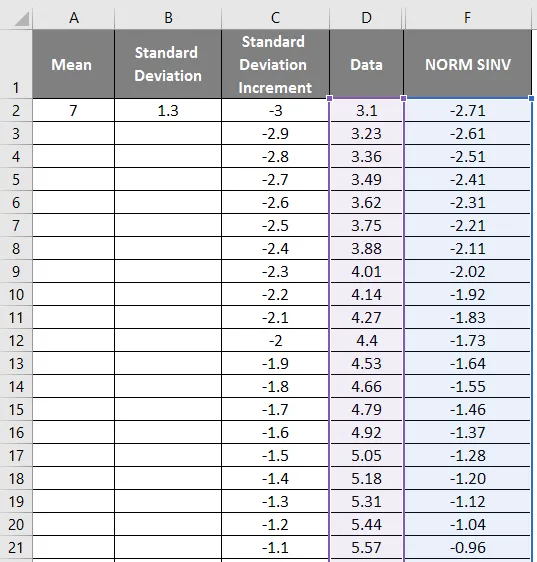
- Najpierw wybierz dane i kolumnę Normalny.
- Przejdź do zakładki Wstaw i wybierz wykres rozproszony.
- Otrzymamy poniższy wykres, który pokazano na poniższym zrzucie ekranu.
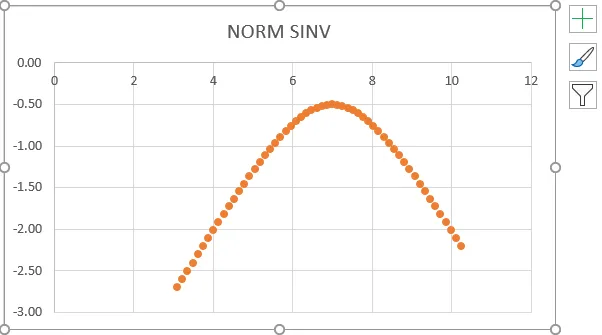
- Z powyższego zrzutu ekranu możemy zobaczyć, że otrzymaliśmy dokładną odwrotność rozkładu normalnego, który pokazuje tę samą wartość pokazaną poniżej.

Przykład # 3 - Konfiguracja lewej i prawej krzywej
W tym przykładzie skonfigurujemy lewą i prawą krzywą za pomocą funkcji rozkładu normalnego. Rozważ poniższe dane, jak pokazano poniżej, gdzie x ma wartości ujemne i zwiększa się do wartości dodatnich.
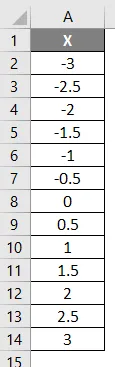
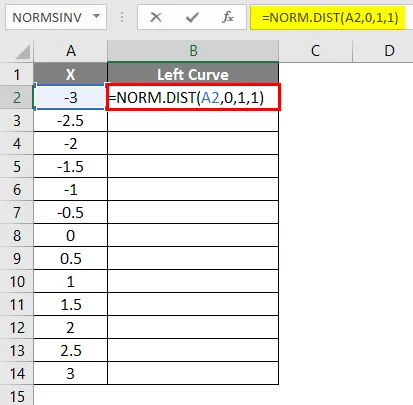
- Zastosuj formułę = NORM.DIST (A2, 0, 1, 1).
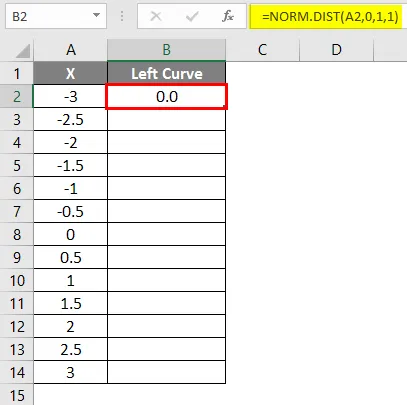
- Po zastosowaniu formuły wynik pokazano poniżej.
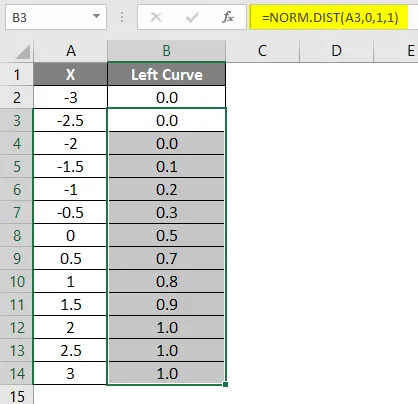
- Przeciągnij formułę do innych komórek.
- Zastosuj formułę = 1-B2 .
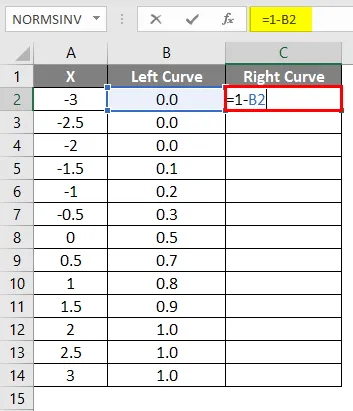
- Po zastosowaniu formuły wynik pokazano poniżej.
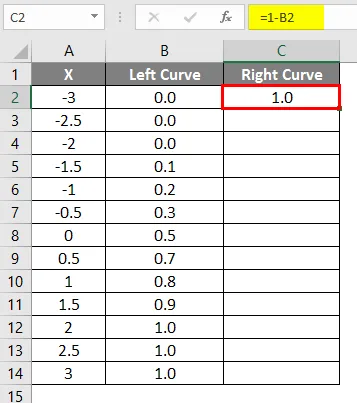
- Przeciągnij tę samą formułę do innych komórek.
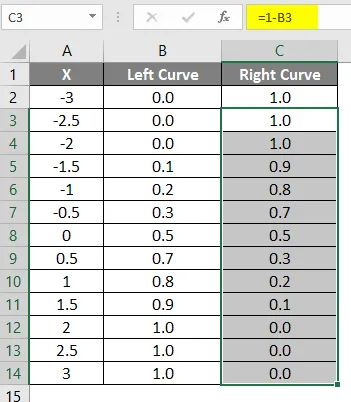
Wynik powyższej zastosowanej formuły pokazano poniżej.
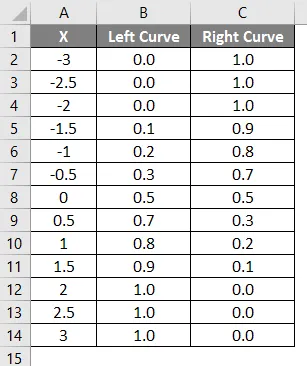
- Wartości lewej krzywej obliczono, stosując formułę NORMALNA DYSTRYBUCJA, ustawiając wartość skumulowaną na True, a NORMSINV obliczono za pomocą lewej krzywej.
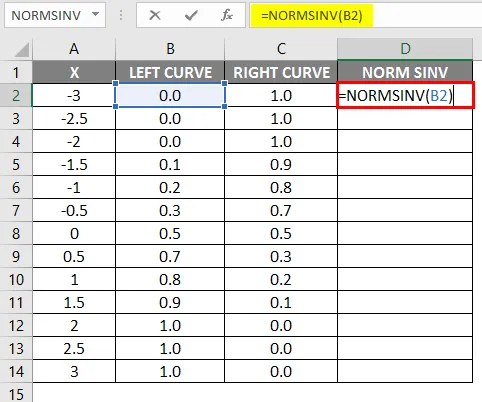
- Po zastosowaniu formuły wynik pokazano poniżej.
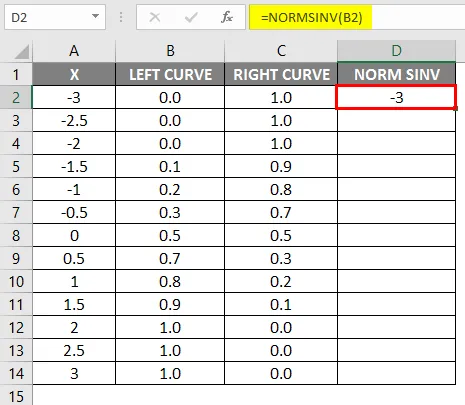
- Przeciągnij tę samą formułę do innych komórek.
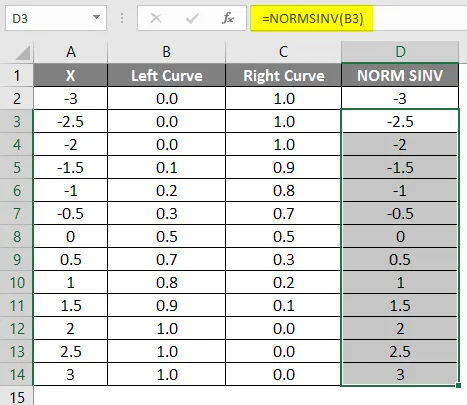
Jak widzimy, otrzymaliśmy taką samą wartość dla NORMSINV, która jest niczym innym jak odwrotnością rozkładu normalnego. W ten sam sposób otrzymamy prawą wartość krzywej, obliczając wartość 1-lewej krzywej. W następnym kroku sprawdzimy, jak uzyskamy wysokość x za pomocą wykresu rozproszonego.
- Wybierz lewą kolumnę utwardzania i prawą krzywą.
- Przejdź do menu wstawiania.
- Wybierz wykres rozproszony w następujący sposób.
Otrzymamy poniższy wynik wykresu, jak pokazano poniżej.
Wykres NORM SINV:
Na poniższym wykresie możemy zobaczyć, że lewa krzywa wartości NORM DISTRIBUTION ma dokładne dopasowanie dla (0, 0, 5), które leży w środku linii, na której otrzymamy ten sam wykres, jeśli złożymy wniosek o NORMDIST.
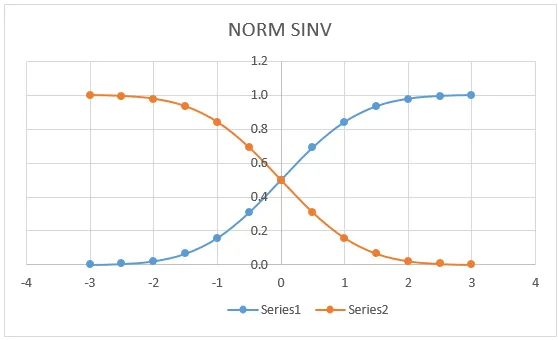
Tutaj na powyższym wykresie bardzo wyraźnie widać, że otrzymaliśmy dokładną średnią w punkcie środkowym, która oznacza:
- X = 0
- Krzywa lewa = 0, 5
- Krzywa prawa = 0, 5
Wyświetliliśmy go, aby wyświetlić wartości NORMSINV w formacie graficznym, jak pokazano poniżej.
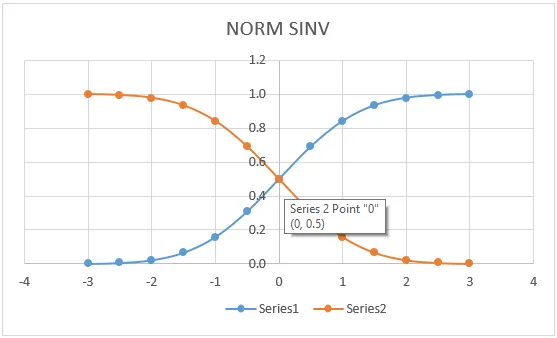
O czym należy pamiętać o programie Excel NORMSINV
- #wartość! Błąd występuje, gdy podany argument jest wartością nienumeryczną lub logiczną.
- W funkcji rozkładu normalnego zwykle otrzymujemy #NUM! błąd wynikający z argumentu odchylenia standardowego jest mniejszy lub równy zero.
Polecane artykuły
To jest przewodnik po programie Excel NORMSINV. Tutaj omawiamy sposób korzystania z NORMSINV w programie Excel wraz z praktycznymi przykładami i szablonem Excela do pobrania. Możesz także przejrzeć nasze inne sugerowane artykuły -
- Jak korzystać z pola nazwy w programie Excel?
- Praca z macierzą w programie Excel
- Co jeśli analiza w programie Excel
- Formuła NPV w programie Excel