
Wzór na złożoną roczną stopę wzrostu (spis treści)
- Formuła
- Przykłady
- Kalkulator
Jaka jest formuła złożonej rocznej stopy wzrostu?
Złożenie to efekt, w którym inwestycja przynosi odsetki nie tylko od głównego składnika, ale także odsetki od odsetek. Tak więc skumulowana roczna stopa wzrostu jest efektywnym rocznym wzrostem osiągniętym z inwestycji, biorąc pod uwagę powiększenie obrazu. Zasadniczo zakłada się, że odsetki naliczane każdego roku są reinwestowane i zarabiają takie same odsetki jak kwota główna. Z tego powodu skumulowana roczna stopa wzrostu jest zawsze wyższa niż zwykła stopa procentowa. Wiele inwestycji, takich jak fundusze wspólnego inwestowania, zwrot z rynku akcji nie są bardzo liniowe i bardzo niestabilne.
Skumulowana roczna stopa wzrostu pomaga w wyrównaniu tego zwrotu i pokaże, ile inwestor zarobił w okresie inwestycji, biorąc pod uwagę fakt, że wszystkie zyski między tym okresem są reinwestowane według tej samej stopy. Ze względu na ten efekt wygładzania pomaga nam porównywać zestawy danych o różnym poziomie zmienności. Jest bardzo często wykorzystywany do celów analizy finansowej.
Końcowa kwota inwestycji = kwota początkowa (1 + CAGR) Liczba lat
Wzór na Skumulowaną roczną stopę wzrostu -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Ta formuła ma zastosowanie, jeśli inwestycja się komplikuje co roku, co oznacza, że inwestujemy pieniądze raz w roku. Ale czasami zdarza się, że chcemy obliczyć stawkę, w której dochodzi do komplikacji co kwartał, miesiąc, codziennie. W tym celu używamy poniższej formuły:
Końcowa kwota inwestycji = kwota początkowa (1 + CAGR / Częstotliwość obliczeniowa) (liczba lat * Częstotliwość obliczeniowa)
Tak więc wzór na Skumulowaną roczną stopę wzrostu -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Częstotliwość mieszania:
- Składanie półroczne: 2
- Składanie kwartalne: 4
- Częstotliwość miesięczna: 12 i tak dalej
Przykłady formuły CAGR (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie wzoru CAGR.
Możesz pobrać ten szablon Excela ze złożoną roczną stopą wzrostu - Szablon Excel ze złożoną roczną stopą wzrostuFormuła CAGR - przykład nr 1
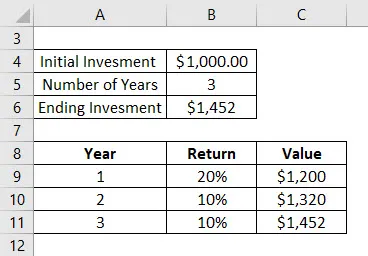
Powiedzmy, że zainwestowałeś 1000 USD w fundusze wspólnego inwestowania 3 lata temu. Oto zwrot, który otrzymałeś przez te 3 lata:
- W pierwszym roku masz 20% wzrost wartości. Łączna wartość wynosi 1200 USD na koniec pierwszego roku
- W drugim roku masz 10% wzrost wartości. Tak więc całkowita wartość wynosi 1320 USD na koniec drugiego roku
- W trzecim roku masz 10% wzrost wartości. Łączna wartość wynosi 1452 USD na koniec trzeciego roku
CAGR oblicza się przy użyciu poniższego wzoru
CAGR = (końcowa kwota inwestycji / kwota początkowa) (1 / liczba lat) - 1
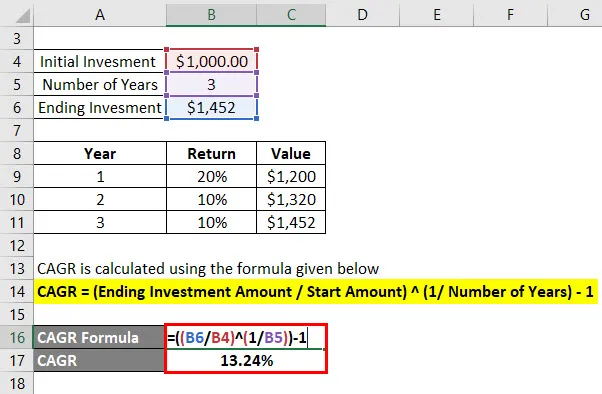
- CAGR = (1452 USD / 1000 USD) (1/3) - 1
- CAGR = 13, 24%
Widzimy tutaj, że roczny zwrot za wszystkie 3 lata jest różny i różny, ale złożona roczna stopa wzrostu daje nam jedną stopę, którą możemy porównać z różnymi możliwościami inwestycyjnymi.
Formuła CAGR - przykład nr 2
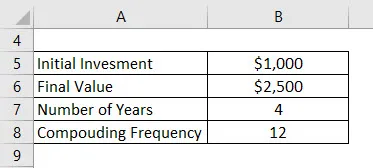
Powiedzmy, że zainwestowałeś 1000 $ w bank i chcesz zatrzymać pieniądze w banku przez 4 lata. Powiedzmy teraz, że łączna kwota, którą otrzymasz po 4 latach, wynosi 2500 USD. Bank oferuje stawki z miesięcznym składaniem. Oblicz CAGR.
CAGR oblicza się przy użyciu poniższego wzoru
CAGR = częstotliwość obliczeniowa * ((końcowa kwota inwestycji / kwota początkowa) (1 / (liczba lat * częstotliwość obliczeniowa)) - 1)
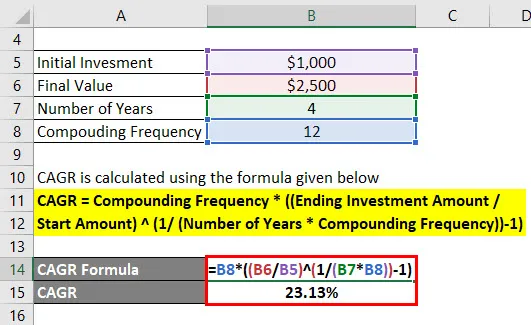
- CAGR = 12 * ((2500 $ / 1000 $) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Tak więc skumulowana roczna stopa wzrostu wynosi 23, 13%.
Wyjaśnienie formuły złożonej rocznej stopy wzrostu
Chociaż złożona roczna stopa wzrostu jest roczną stopą inwestycji, jest to jedynie wartość teoretyczna i nie jest prawdziwym zwrotem. Głównym założeniem jest to, że wszystkie zyski są reinwestowane według tej samej stopy w okresie inwestycyjnym, ale stopa ta nie pozostanie przez wszystkie lata i nie możemy inwestować naszych pieniędzy według tej samej stopy. Jest to więc jedyna reprezentatywna stawka, która mówi nam, że moglibyśmy skończyć, gdyby wszystkie pieniądze były reinwestowane pod koniec każdego roku według tej stawki. Jest zatem kilka kluczowych punktów, które powinniśmy wziąć pod uwagę, stosując złożoną roczną stopę wzrostu.
Będziemy również bardzo ostrożni z inwestycją, która ma długi okres. Na przykład, jeśli okres inwestycji jest bardzo długi, powiedzmy 20 lat, skumulowana roczna stopa procentowa może dać nam błędne wskazanie, ponieważ może się zdarzyć, że nie osiągamy żadnych zysków przez pierwsze 15 lat, a wszystkie zwroty przychodzą w ostatnim okresie . Nie można zarabiać przez 15 lat bez zysków.
Podobnie, jeśli dwie możliwości inwestycyjne mają ten sam CAGR, może się zdarzyć, że jedna będzie bardziej przyciągana niż druga z powodu tego, że wzrost w jednej następuje w początkowym okresie, podczas gdy w drugiej jest skoncentrowany pod koniec okresu Kropka.
Trafność i zastosowania formuły złożonej rocznej stopy wzrostu
Złożona roczna stopa wzrostu jest naprawdę pomocna w obliczaniu średniej stopy wzrostu inwestycji i może pomóc w porównaniu różnych inwestycji. Jak widzieliśmy w powyższym przykładzie, wzrost inwestycji z roku na rok jest nierówny i nieregularny. Ale stosując złożoną roczną stopę wzrostu, zwrot wygładza się. Innym czynnikiem, który sprawia, że skumulowana roczna stopa wzrostu jest krytyczną metodą przy określaniu wzrostu inwestycji, jest to, że bierze pod uwagę efekt mieszania, którego nie osiąga roczna stopa zwrotu. Złożona roczna stopa nie daje nam rzeczywistego obrazu zwrotu, ponieważ oblicza jedynie zwrot z kwoty głównej i ignoruje odsetki od komponentu odsetkowego, ale nie jest tak w przypadku złożonej rocznej stopy wzrostu.
Złożony roczny kalkulator formuły wzrostu
Możesz użyć następującego kalkulatora rocznego skumulowanego wzrostu gospodarczego
| Końcowa kwota inwestycji | |
| Kwota początkowa | |
| Liczba lat | |
| CAGR | |
| CAGR = | ((Końcowa kwota inwestycji / Kwota początkowa) 1 / Liczba lat -1) |
| = | ((0/0) 1/0 -1) = 0 |
Polecane artykuły
Jest to przewodnik po formule Skumulowanego rocznego tempa wzrostu. Tutaj omawiamy sposób obliczania CAGR wraz z praktycznymi przykładami. Oferujemy również kalkulator Skumulowanego rocznego tempa wzrostu z szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przewodnik po formule stopy zwrotu
- Przykłady wzoru wzrostu wykładniczego
- Kalkulator dla wzoru twierdzenia o granicy centralnej
- Jak obliczyć kapitalizację rynkową?