
Wprowadzenie do serii Fibonacciego w Pythonie
Seria Fibonacciego w Pythonie, jest to określane jako seria liczb, gdzie następna liczba jest sumą dwóch obecnych liczb.
Na przykład:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. itd
Więc tutaj 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 i tak dalej.
Patrząc na powyższe, można mieć pewne pojęcie o tym, o czym mówimy.
Jednak pod względem reguły matematycznej można ją zapisać jako:

Gdzie n-ta liczba jest sumą liczby w miejscach (n-1) i (n-2). Jeśli chodzi o wdrożenie serii Fibonacciego, może istnieć wiele języków kodowania, za pomocą których można to zrobić.
Jednak Python jest obecnie powszechnie używanym językiem. Zobaczmy implementację serii Fibonacciego przez Python. Zanim przejdziesz dalej, powinieneś być świadomy podstawowych instrukcji warunkowych, takich jak pętla, if-else, while loop itp. W Pythonie. Jeśli nie, byłoby wspaniale, gdyby ktoś mógł to zmienić, a następnie zająć się nadchodzącą treścią. Tutaj dla celów demonstracyjnych używam spyder, który jest IDE dla języka programowania Python. Do wykonywania programów w języku Python można także używać dowolnych innych notesów IDE lub Ipython.
Seria Fibonacciego w języku Python
Zobaczmy implementację liczby Fibonacciego i Serii, biorąc pod uwagę, że 1. dwa elementy Fibonacciego to 0 i 1:
Możesz jednak dostosować funkcję Fibonacciego według własnych wymagań, ale najpierw zapoznaj się z podstawami i stopniowo przechodź do innych.
Kod Python do znalezienia n-tej liczby Fibonacciego
Kod 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Kod 2:
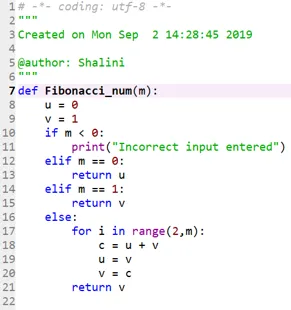
Wynik:
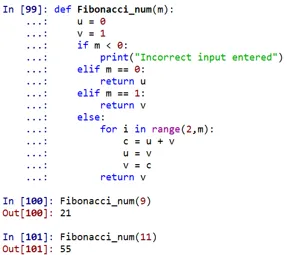
Jak widać, liczba Fibonacciego na 9 miejscu wynosiłaby 21, a na 11 miejscu 55.
- Tutaj „fibonacci_num” jest zdefiniowaną funkcją, która dba o znalezienie liczby Fibonacciego za pomocą określonych warunków. Tę funkcję można wywołać, określając dowolną pozycję.
Zobaczmy teraz, jak można wydrukować serie, aż do wspomnianej pozycji:
Kod:
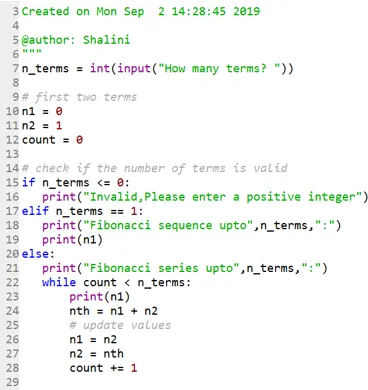
Wynik:
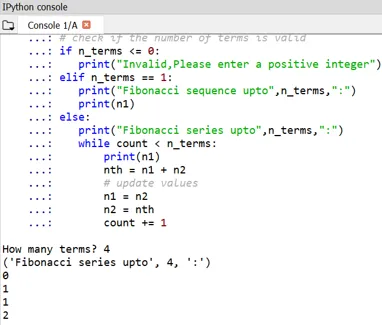
Można zauważyć, że początek liczb Fibonacciego jest zdefiniowany jako 0 i 1.
- Jeśli ktoś chce zdefiniować własne warunki początkowe, można to zrobić w ten sam sposób, dostosowując n1 i n2. Oto przykład:
Powiedzmy teraz, że chcemy, aby nasze warunki początkowe były następujące: n1 = 3, n2 = 5
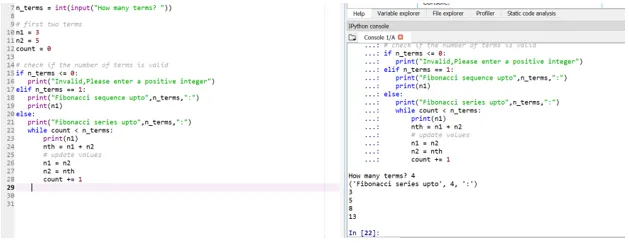
Więc tutaj twoja pozycja 4 kadencji (podejmowane są przez użytkownika) zostanie ustalona na podstawie twoich warunków początkowych.
Metody, za pomocą których można wygenerować serię Fibonacciego
Poniżej znajdują się trzy metody, za pomocą których można wygenerować serię Fibonacciego:
1. Poprzez generatory
Kod:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Wynik:
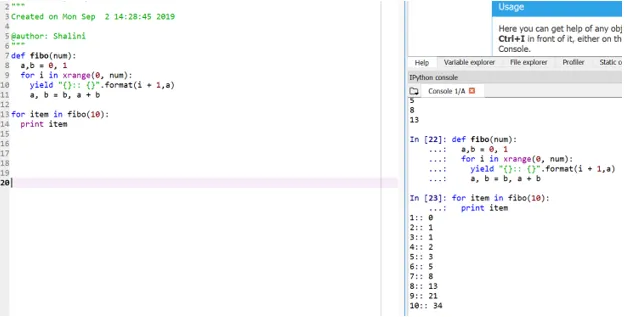
Ta metoda jest nazywana „generatorem”, ponieważ funkcja xrange jest generatorem liczb od 0 do num, a fed jest generatorem sformatowanego wyjścia.
Oto, co xrange robi dla Ciebie:

Tutaj szereg Fibonacciego został zdefiniowany w postaci funkcji, w której dla funkcji pętli, xrange i funkcji wydajności dba o wynik.
2. Przez pętlę for
Kod:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Wynik:

Jak widać, do wypisania szeregu Fibonacciego z zakresu od 0 do 10. użyto prostej dla pętli. Wewnątrz dla pętli zmienne zostały przypisane nowe wartości. U i v to domyślne wartości początkowe Fibonacciego, które zostały ustawione odpowiednio na 0 i 1.
Gdy pętla postępuje do uruchomienia, nowa wartość u jest starą wartością v, podczas gdy nowa wartość v jest sumą starych wartości u i v. Trwa to do końca wartości zakresu.
3. Poprzez rekurencję
Kod:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Wynik:
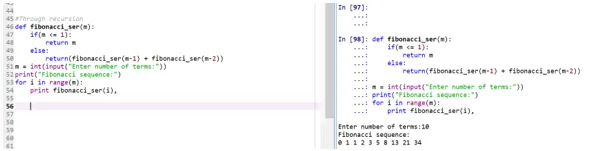
- Funkcja „fibonacci_ser” wywołuje samą siebie, aby wydrukować serię Fibonacciego.
- I stąd metoda ma swoją nazwę „rekurencja”.
Kroki, które wykonano tutaj:
- Tutaj użytkownik został poproszony o podanie miejsca, do którego należy wydrukować serię Fibonacciego.
- Liczba przechodzi przez funkcję „fibonacci_ser”.
- Warunek zostanie sprawdzony, jeśli podana długość jest mniejsza niż 1 lub nie. Jeśli tak, wynik jest podawany natychmiast.
- Jeśli jednak długość jest większa niż 1, wywoływane są rekurencyjne wywołania „fibonacci_ser” z argumentami o długości mniejszej niż 1 i 2, tj. Fibonacci_ser (m-1) i fibonacci_ser (m-2).
- Dlatego rekurencja daje pożądany wynik i wydrukuje go.
- Krótko mówiąc, omówiliśmy Trzy sposoby wyświetlania serii Fibonacciego.
- Przez pętlę for, generatory i rekurencję.
Podsumowanie wszystkich trzech kodów Pythona
Poniżej znajdują się trzy kody python:
1. Poprzez generatory
Kod:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Przez pętlę for
Kod:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Poprzez rekurencję
Kod:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Podsumowane powyżej są wszystkie procedury, trzeba poćwiczyć, aby dobrze się nimi posługiwać.
Wynik:
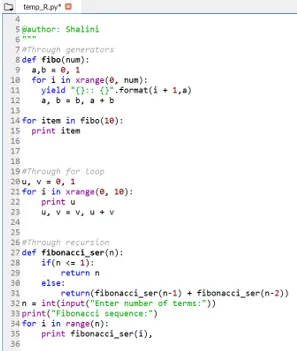
Wniosek
Przeglądając powyższą zawartość Fibonacciego, ktoś miałby krystalicznie czyste zrozumienie liczb i serii Fibonacciego, specjalizujących się w pythonie. Kiedyś zaznajamia się z logiką serii Fibonacciego, generując kolejny zestaw serii, pracując z innymi liczbami i różnymi metodami, będzie teraz dla ciebie bułką z masłem. Logiczne podejście jest jedynym sposobem na osiągnięcie doskonałości.
Polecane artykuły
Jest to przewodnik po serii Fibonacciego w Pythonie. Tutaj omawiamy liczby i serie Fibonacciego, specjalizujące się w pythonie, generujące kolejny zestaw serii, pracujące z innymi liczbami i różnymi metodami. Możesz również przejrzeć nasze inne powiązane artykuły, aby dowiedzieć się więcej -
- Generator liczb losowych w Pythonie
- Funkcje matematyczne w języku Python
- Silnia w Pythonie
- Hermetyzacja w Pythonie
- Seria Fibonacciego w Javie
- Funkcje Pythona
- Program czynnikowy w JavaScript
- Generator liczb losowych w Matlabie
- Generator liczb losowych w C #
- Hermetyzacja w JavaScript