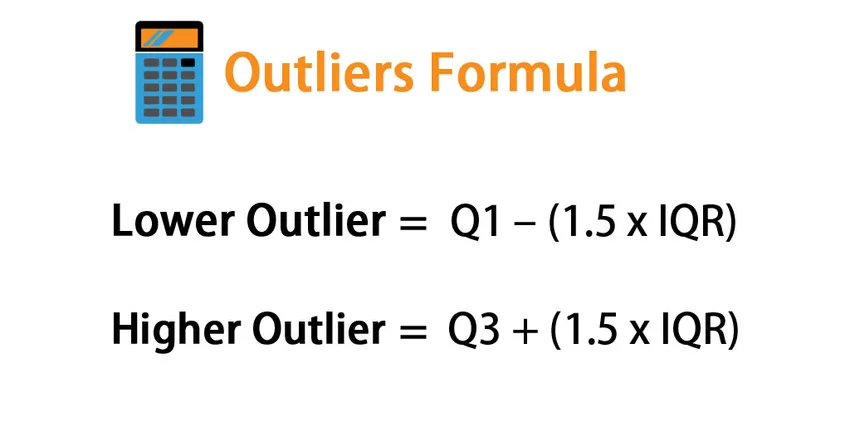
Formuła wartości odstających (spis treści)
- Formuła wartości odstających
- Przykłady formuły wartości odstających (z szablonem Excel)
Formuła wartości odstających
W statystykach wartości odstające są dwoma skrajnie odległymi nietypowymi punktami w danych zbiorach. Ekstremalnie wysoka i bardzo niska wartość są wartościami odstającymi zestawu danych. Jest to bardzo przydatne w wykrywaniu wszelkich błędów i pomyłek. Jak sama nazwa wskazuje, wartości odstające to wartości leżące poza resztą wartości w zbiorze danych. Przykład: rozważ studentów inżynierii i wyobraź sobie, że mieli krasnoludy w swojej klasie. Tak więc krasnoludy to ludzie, którzy mają wyjątkowo niski wzrost w porównaniu z innymi ludźmi o normalnym wzroście. To jest wartość odstająca w tej klasie. Wartości odstające można obliczyć przy użyciu metody Tukeya.
Wzór na wartości odstające -
Lower Outlier = Q1 – (1.5 * IQR)
Higher Outlier= Q3 + (1.5 * IQR)
Przykłady formuły wartości odstających (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie wzoru na wartości odstające.
Możesz pobrać ten szablon wartości odstających tutaj - szablon wartości odstającychFormuła wartości odstających - przykład nr 1
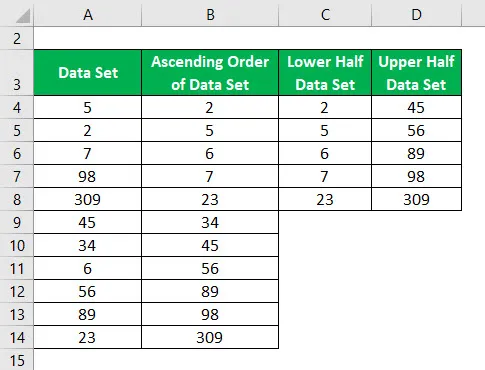
Rozważ następujący zestaw danych i oblicz wartości odstające dla zestawu danych.
Zestaw danych = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23
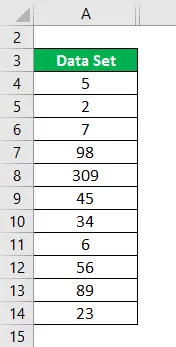
Rosnąco uporządkowany zestaw danych:
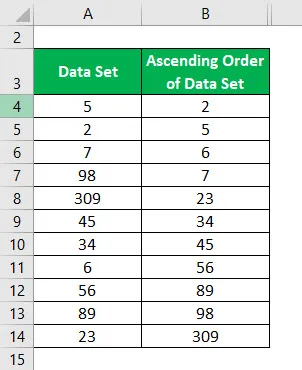
Mediana zbioru danych zamówienia rosnącego jest obliczana jako:
W tym zestawie danych całkowita liczba danych wynosi 11. Więc n = 11. Mediana = 11 + 1/2 = 12/2 = 6. Stąd wartością, która znajduje się na 6. pozycji w tym zestawie danych jest mediana.
Zatem wartość mediany = 34.
Podziel zestaw danych na 2 połowy za pomocą mediany.
Mediana zbioru danych dolnej połowy i górnej połowy jest obliczana jako:
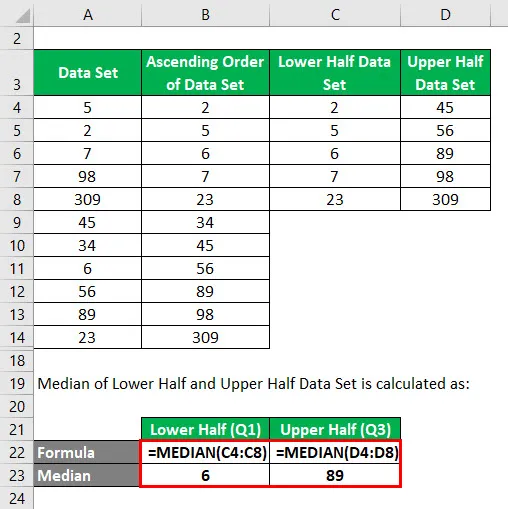
- W dolnej połowie 2, 5, 6, 7, 23, jeśli znajdziemy medianę podobną do tej z kroku 2, mediana będzie wynosić 6. Zatem Q1 = 6.
- W górnej połowie 45, 56, 89, 98 309, jeśli znajdziemy medianę podobną do tej z kroku 2, wartość mediany wyniesie 89. Zatem Q3 = 89.
IQR jest obliczany przy użyciu poniższego wzoru
IQR = Q3 - Q1
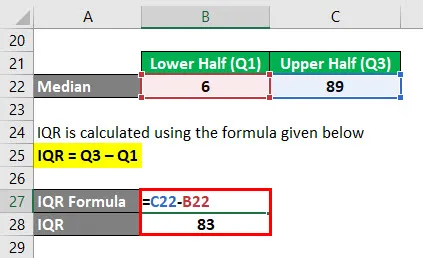
- IQR = 89–6
- IQR = 83
Dolna wartość odstająca jest obliczana przy użyciu poniższego wzoru
Dolna wartość odstająca = Q1 - (1, 5 * IQR)
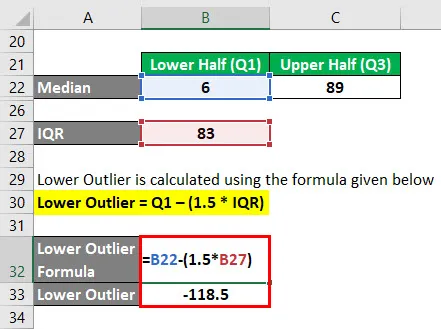
- Dolna wartość odstająca = 6 - (1, 5 * 83)
- Dolna wartość odstająca = -118, 5
Wyższa wartość odstająca jest obliczana przy użyciu poniższego wzoru
Wyższa wartość odstająca = Q3 + (1, 5 * IQR)
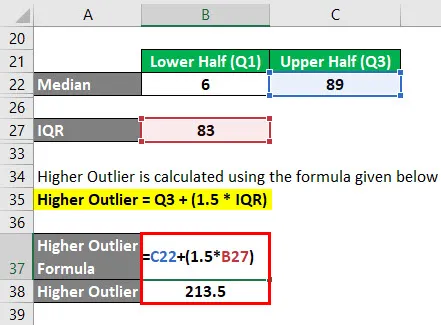
- Wyższa wartość odstająca = 89 + (1, 5 * 83)
- Wyższa wartość odstająca = 213, 5
Teraz pobierz te wartości z zestawu danych -118, 5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213, 5, 309. Wartości, które spadają poniżej dolnej wartości i powyżej górnej są wartością odstającą. Dla tego zestawu danych wartość 309 jest wartością odstającą.
Formuła wartości odstających - przykład 2
Rozważ następujący zestaw danych i oblicz wartości odstające dla zestawu danych.
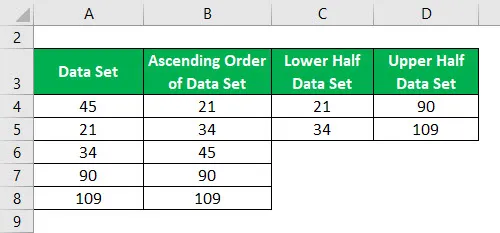
Zestaw danych = 45, 21, 34, 90, 109.
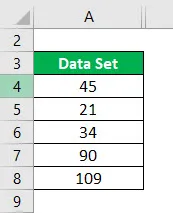
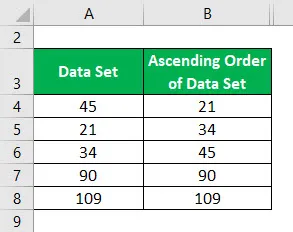
Rosnąco uporządkowany zestaw danych:
Mediana zbioru danych zamówienia rosnącego jest obliczana jako:
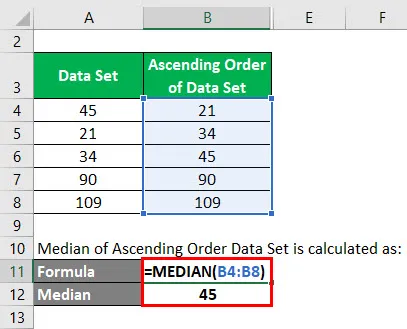
W tym zestawie danych całkowita liczba danych wynosi 5. Więc n = 5. Mediana = 5 + 1/2 = 6/2 = 3. Stąd wartością, która znajduje się na 3. pozycji w tym zestawie danych jest mediana.
Zatem wartość mediany = 45.
Podziel zestaw danych na 2 połowy za pomocą mediany.
Mediana zbioru danych dolnej połowy i górnej połowy jest obliczana jako:
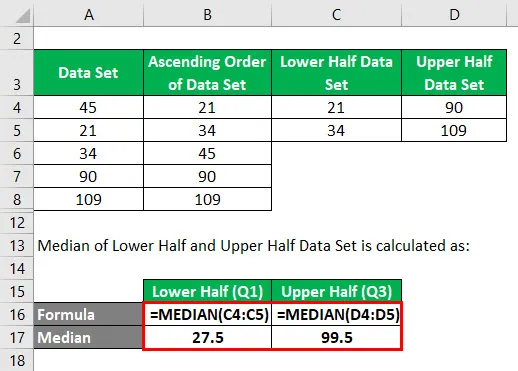
- Q1 = 27, 5
- Q3 = 89
IQR jest obliczany przy użyciu poniższego wzoru
IQR = Q3 - Q1
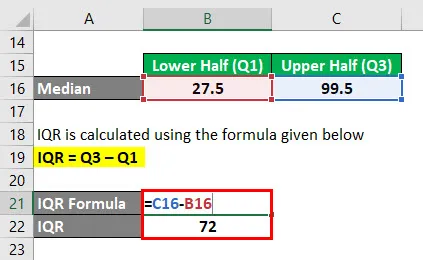
- IQR = 99, 5 - 27, 5
- IQR = 72
Dolna wartość odstająca jest obliczana przy użyciu poniższego wzoru
Dolna wartość odstająca = Q1 - (1, 5 * IQR)
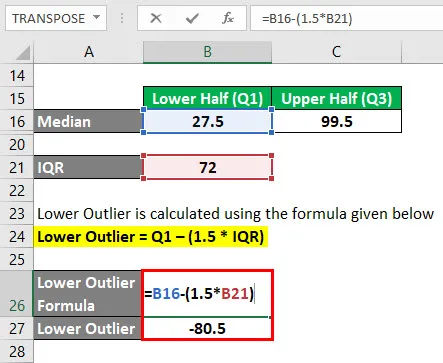
- Dolna wartość odstająca = 27, 5 - (1, 5 * 72)
- Dolna wartość odstająca = -80, 5
Wyższa wartość odstająca jest obliczana przy użyciu poniższego wzoru
Wyższa wartość odstająca = Q3 + (1, 5 * IQR)
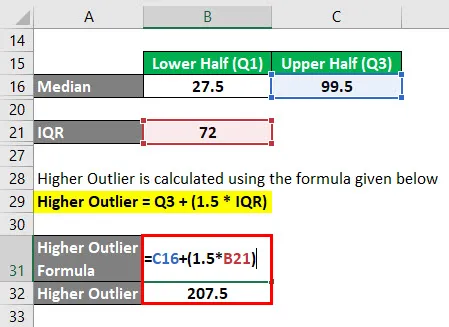
- Wyższa wartość odstająca = 99, 5 + (1, 5 * 72)
- Wyższa wartość odstająca = 207, 5
Wyjaśnienie
Krok 1: Ułóż wszystkie wartości w danym zestawie danych w porządku rosnącym.
Krok 2: Znajdź wartość mediany dla sortowanych danych. Medianę można znaleźć za pomocą następującego wzoru. Poniższe obliczenia przedstawiają po prostu pozycję wartości mediany, która znajduje się w zestawie dat.
Mediana = (n + 1) / 2
Gdzie n jest całkowitą liczbą danych dostępnych w zbiorze danych.
Krok 3: Znajdź niższą wartość kwartylu Q1 ze zbioru danych. Aby to znaleźć, używając wartości mediany podziel zestaw danych na dwie połowy. Z dolnej połowy zestawu wartości znajdź medianę dla tego niższego zestawu, którym jest wartość Q1.
Krok 4: Znajdź górną wartość kwartylu Q3 ze zbioru danych. Jest dokładnie tak jak powyższy krok. Zamiast dolnej połowy musimy postępować zgodnie z tą samą procedurą, co zestaw wartości górnej połowy.
Krok 5: Znajdź wartość IQR zakresu międzykwartylowego. Aby znaleźć wartość Odliczenia Q1 z Q3.
IQR = Q3-Q1
Krok 6: Znajdź wartość Inner Extreme. Koniec, który wypada poza dolną stronę, który można również nazwać niewielką wartością odstającą. Pomnóż wartość IQR przez 1, 5 i odejmij tę wartość od Q1, otrzymując wewnętrzną dolną skrajność.
Dolna wartość odstająca = Q1 - (1, 5 * IQR)
Krok 7: Znajdź wartość Outer Extreme. Koniec, który wypada poza wyższą stronę, który można również nazwać dużą wartością odstającą. Pomnożenie wartości IQR przez 1, 5 i zsumowanie tej wartości z Q3 daje Outer Higher Extreme.
Wyższa wartość odstająca = Q3 + (1, 5 * IQR)
Krok 8: Wartości, które wykraczają poza te skrajności wewnętrzne i zewnętrzne, są wartościami odstającymi dla danego zestawu danych.
Formuła przydatności i zastosowań wartości odstających
Wartości odstające są bardzo ważne w każdym problemie z analizą danych. Wartość odstająca wykazuje niespójność w dowolnym zbiorze danych, ponieważ jest zdefiniowany jako niezbyt odległe wartości w zbiorze danych od jednego do drugiego. Jest to bardzo przydatne w znajdowaniu jakichkolwiek błędów, które wystąpiły w zbiorze danych. Ponieważ po umieszczeniu błędu w zbiorze danych wpływa to na średnią, a zatem mediana może powodować duże odchylenia w wyniku, jeśli wartości odstające znajdują się w zbiorze danych. Dlatego konieczne jest ustalenie wartości odstających z zestawu danych, aby uniknąć poważnych problemów w analizie statystycznej.
Polecane artykuły
To był przewodnik po formule wartości odstających. Tutaj omawiamy sposób obliczania wartości odstających wraz z praktycznymi przykładami i szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przewodnik po formule Midrange
- Przykłady wzoru wynagrodzenia
- Kalkulator Formuły DPMO
- Jak obliczyć rozkład T?
- Wzór na odchylenie kwartylowe | Przykłady