
Wzór na współczynnik zmienności (spis treści)
- Formuła
- Przykłady
Jaki jest wzór współczynnika zmienności?
W statystyce współczynnik zmienności określany również jako CV jest narzędziem, które pomaga nam określić, w jaki sposób punkty danych w zbiorze danych są rozmieszczone wokół średniej. Zasadniczo najpierw wykreślane są wszystkie punkty danych, a następnie współczynnik zmienności jest wykorzystywany do pomiaru dyspersji tych punktów od siebie i średniej. Pomaga nam to zrozumieć dane, a także zobaczyć wzór, który tworzy. Oblicza się go jako stosunek odchylenia standardowego zestawu danych do wartości średniej. Wyższy współczynnik zmienności oznacza, że istnieje większy poziom rozproszenia danych wokół średniej. Podobnie, niższa wartość współczynnika zmienności, mniejsza dyspersja i dokładniejsze wyniki. Nawet jeśli średnia z dwóch serii danych jest znacznie różna, współczynnik zmienności jest bardzo przydatny do porównania stopnia zmienności z jednej serii danych do drugiej.
Wzór na współczynnik zmienności podaje:
Coefficient of Variation = Standard Deviation / Mean
Kroki do obliczenia współczynnika zmienności:
Krok 1: Oblicz średnią zestawu danych. Średnia jest średnią wszystkich wartości i można ją obliczyć, biorąc sumę wszystkich wartości, a następnie dzieląc ją przez liczbę punktów danych.
Krok 2: Następnie oblicz standardowe odchylenie zestawu danych. To trochę czasochłonny proces. Odchylenie standardowe można obliczyć jako: √ (Σ (X i - X m ) 2 / (n - 1)) . X i jest i -tym punktem danych, a X m jest średnią zestawu danych. Alternatywnie możemy również znaleźć odchylenie standardowe w programie Excel za pomocą funkcji STDEV.S ().
Krok 3: Podziel odchylenie standardowe, aby uzyskać współczynnik zmienności.
Przykłady formuły współczynnika zmienności (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie współczynnika zmienności.
Możesz pobrać szablon Excel Formula współczynnika zmienności tutaj - szablon Excel Formula współczynnika zmiennościWzór na współczynnik zmienności - przykład nr 1
Załóżmy, że mamy dwa zestawy danych A i B, z których każdy zawiera 20 losowych punktów danych. Obliczyć współczynnik zmienności dla zbioru danych X i Y.
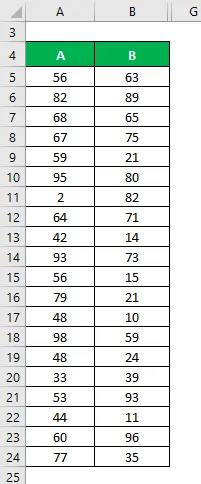
Rozwiązanie:
Średnia jest obliczana jako:
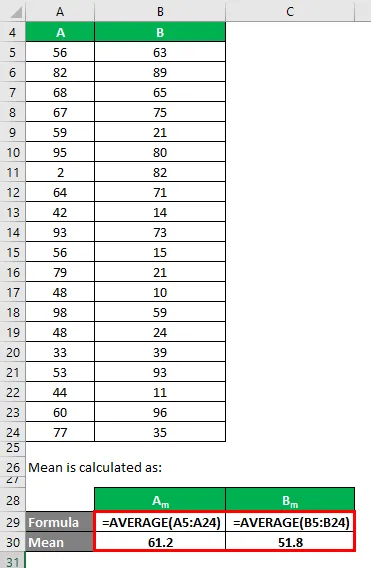
- Średnia zestawu danych A = 61, 2
- Średnia zestawu danych B = 51, 8
Teraz musimy obliczyć różnicę między punktami danych a wartością średnią.
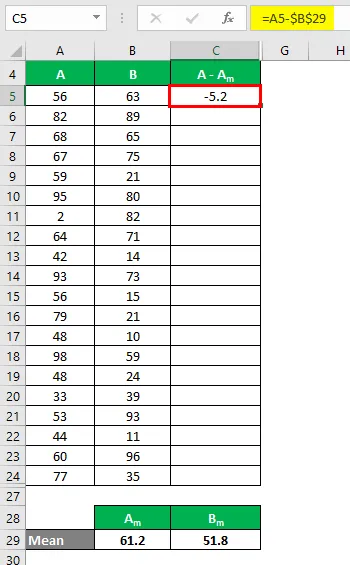
Podobnie obliczyć dla wszystkich wartości zestawu danych A.
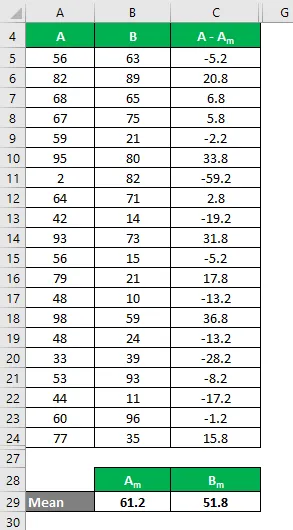
Podobnie obliczyć dla wszystkich wartości zestawu danych B.
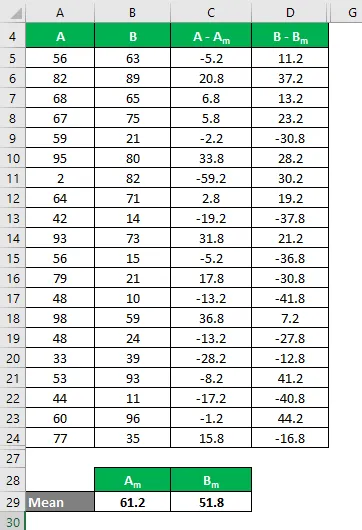
Oblicz kwadrat różnicy dla obu zestawów danych A i B.
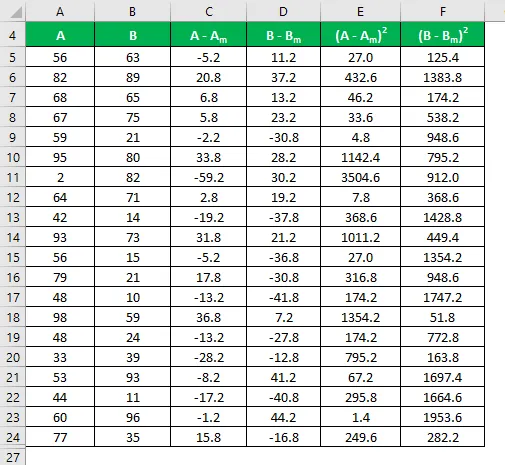
Odchylenie standardowe jest obliczane przy użyciu poniższego wzoru
Odchylenie standardowe = √ (Σ (X i - X m ) 2 / (n - 1))
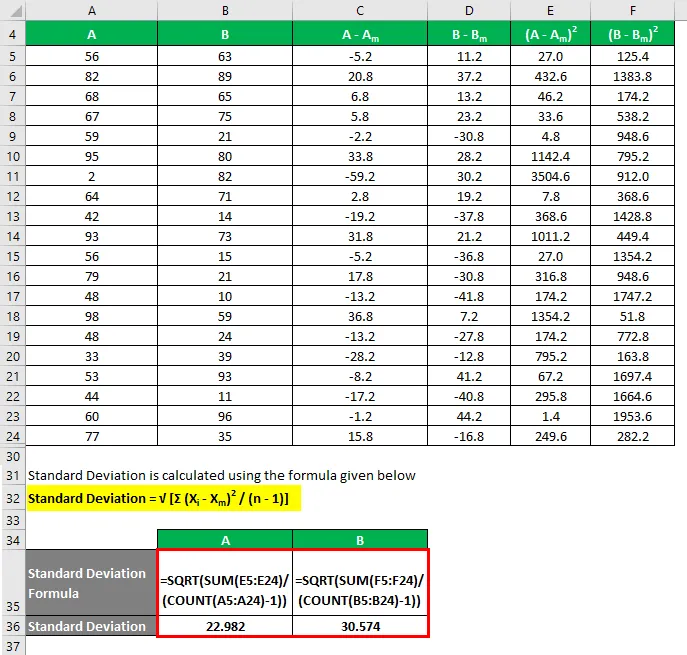
Współczynnik zmienności jest obliczany przy użyciu poniższego wzoru
Współczynnik zmienności = odchylenie standardowe / średnia
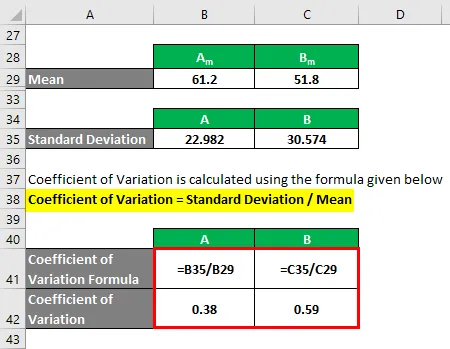
- Współczynnik wariancji A = 22, 982 / 61, 2 = 0, 38
- Współczynnik wariancji B = 30, 574 / 51, 8 = 0, 59
Więc jeśli tu zobaczysz, B ma wyższy współczynnik zmienności niż A, co oznacza, że punkty danych B są bardziej rozproszone niż A.
Wzór na współczynnik zmienności - przykład nr 2
Powiedzmy, że jesteś bardzo niechętnym do inwestowania inwestorem i chcesz zainwestować pieniądze na giełdzie. Ponieważ twój apetyt na ryzyko jest niski, chcesz inwestować w bezpieczne zapasy, które mają niższe odchylenie standardowe i współczynnik zmienności. Zakwalifikowałeś 3 akcje na podstawie ich podstawowych i technicznych informacji i chcesz wybrać 2 akcje. Zebrałeś również informacje o ich historycznych zwrotach z ostatnich 15 lat.
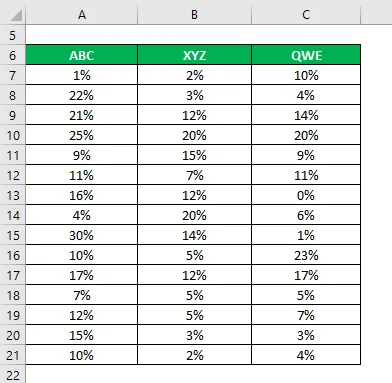
Rozwiązanie:
Średnia jest obliczana jako:
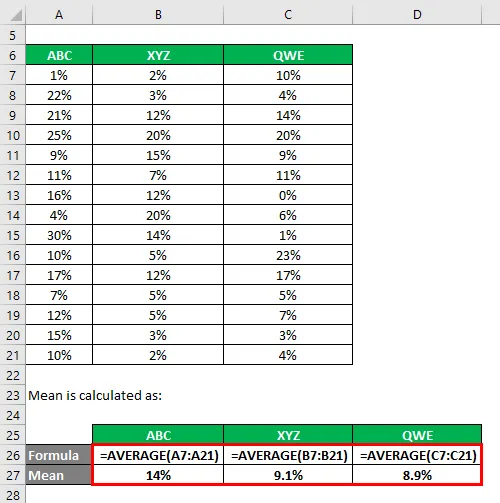
Odchylenie standardowe jest obliczane przy użyciu formuły programu Excel
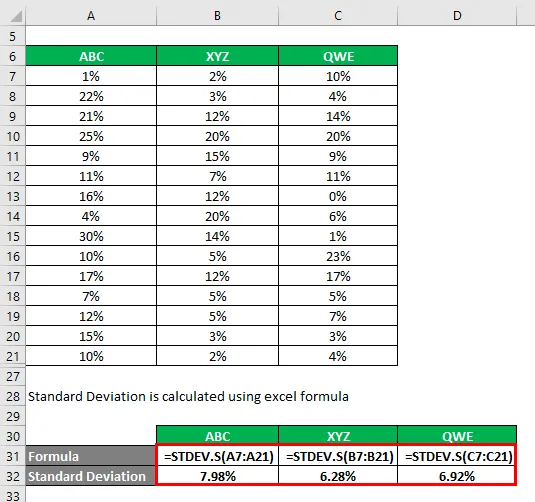
Współczynnik zmienności jest obliczany przy użyciu poniższego wzoru
Współczynnik zmienności = odchylenie standardowe / średnia
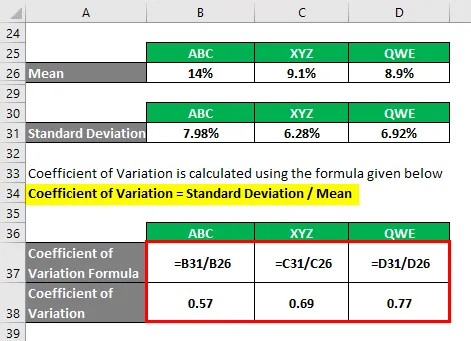
- Współczynnik zmienności ABC = 7, 98% / 14% = 0, 57
- Współczynnik zmienności XYZ = 6, 28% / 9, 1% = 0, 69
- Współczynnik zmienności QWE = 6, 92% / 8, 9% = 0, 77
Na podstawie tych informacji wybierzesz akcje ABC i XYZ do zainwestowania, ponieważ mają one najniższy współczynnik zmienności.
Wyjaśnienie
Ponieważ współczynnik zmienności jest miarą ryzyka, pomaga on zmierzyć zmienność cen akcji i innych instrumentów finansowych. Pomaga także inwestorom i analitykom w porównywaniu ryzyk związanych z różnymi potencjalnymi inwestycjami.
Współczynnik zmienności jest podobny do odchylenia standardowego, ale odchylenie standardowe dwóch zmiennych nie może być użyteczne. Ale zastosowanie odchylenia standardowego i średniej czyni porównanie względne bardziej znaczącym. Istnieje również ograniczenie współczynnika zmienności. Załóżmy, że średnia zestawu danych wynosi zero. W takim przypadku to narzędzie stanie się nieskuteczne. Co więcej, jeśli mamy zbiór danych, który ma wiele wartości dodatnich i ujemnych, współczynnik zmienności staje się bardzo problematyczny. Jest to więc bardziej przydatne w zestawach danych mających ten sam znak plus-minus.
Trafność i zastosowania wzoru współczynnika zmienności
Współczynnik zmienności ma znaczenie w wielu innych dziedzinach niż statystyka. Na przykład w dziedzinie finansów współczynnik zmienności jest miarą ryzyka. Jest podobny do odchylenia standardowego, ponieważ jest on również stosowany jako miara ryzyka, ale różnica polega na tym, że współczynnik zmienności jest lepszym wskaźnikiem ryzyka względnego. Na przykład, powiedzmy, że oczekiwany zwrot A wynosi 15%, a oczekiwany zwrot B wynosi 10%, a A ma odchylenie standardowe 10%, podczas gdy B ma odchylenie standardowe 5%. Aby wybrać lepszą inwestycję, można zastosować współczynnik zmienności. Zatem współczynnik zmienności A wynosi 10/15 = 0, 666, a współczynnik zmienności B wynosi 5/10 = 0, 5. Więc B jest lepszą inwestycją niż A.
Polecane artykuły
To był przewodnik po formule współczynnika zmienności. Tutaj omawiamy sposób obliczania współczynnika zmienności za pomocą wzoru wraz z praktycznymi przykładami i szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Co to jest skorygowana formuła R do kwadratu?
- Przykłady wzoru współczynnika determinacji
- Jak obliczyć współczynnik korelacji za pomocą wzoru?
- Formuła kowariancji z szablonem Excel