Wprowadzenie do sortowania sterty w C
Sortowanie to technika polegająca na porządkowaniu elementów na podstawie różnych właściwości. (Właściwości takie jak porządkowanie danych w porządku rosnącym, malejącym lub alfabetycznym). Jednym z głównych przykładów sortowania, o którym możemy tutaj myśleć, jest zamawianie przedmiotów podczas zakupów online. Możemy odnosić się do cen, popularności, najnowszych i tak dalej. Istnieje wiele technik pozycjonowania elementów poprzez sortowanie. W tym temacie dowiemy się o sortowaniu sterty w C.
Nauczymy się jednej z najpopularniejszych technik sortowania, Heap Sort, w języku programowania C.
Logika sortowania sterty
Jak właściwie możemy wykonać sortowanie sterty? Sprawdźmy poniżej.
Po pierwsze, sterta jest jedną z drzewiastych struktur danych. Zaangażowane tutaj drzewo jest zawsze kompletnym drzewem binarnym. I są dwa rodzaje sterty
- Min - sterty: Ogólnie ułożone w porządku rosnącym, to znaczy, jeśli element węzła nadrzędnego ma wartość mniejszą niż wartość elementów węzła podrzędnego.
- Max - Heap: Ogólnie ułożone w kolejności malejącej, to znaczy, jeśli element węzła nadrzędnego ma wartość większą niż wartość elementów węzła podrzędnego.
Kroki do sortowania sterty
- Po uzyskaniu nieposortowanych danych listy elementy są organizowane w strukturze danych sterty na podstawie utworzenia stosu minimalnego lub maksymalnego.
- Pierwszy element z powyższej listy został dodany do naszej tablicy
- Ponownie formuje się technikę struktury danych głowy tak samo jak w pierwszym kroku i ponownie albo najwyższy element, albo najmniejszy element jest pobierany i dodawany do naszej tablicy.
- Powtarzane kroki pomagają nam uzyskać tablicę z posortowaną listą.
Program sortowania sterty w C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Najpierw prosimy użytkownika o podanie liczby elementów branych do sortowania, a następnie użytkownik może wprowadzić różne elementy, które mają zostać posortowane.
Wykonane kroki
- Następnie skupiamy się na utworzeniu tablicy sterty, w tym przypadku tablicy max-sterty.
- Głównym warunkiem uzyskania tablicy z maksymalną stertą jest sprawdzenie, czy żadna wartość węzła nadrzędnego nie jest mniejsza niż wartość węzła podrzędnego. Zamienimy się, dopóki nie osiągniemy tego warunku.
- Główną zaletą tego pełnego drzewa binarnego jest to, że do lewego i prawego węzła potomnego węzła nadrzędnego można uzyskać odpowiednio wartości 2 (i) + 1 i 2 * (i) + 2. Gdzie i jest węzłem nadrzędnym.
- W ten sposób umieszczamy tutaj nasz węzeł główny, który zawiera maksymalną wartość w najbardziej prawym miejscu węzła liścia. Następnie ponownie postępując zgodnie z tą samą procedurą, tak że następna maksymalna liczba staje się teraz węzłem głównym.
- Będziemy postępować zgodnie z tą samą procedurą, dopóki w tablicy stosu nie pozostanie tylko jeden węzeł.
- Następnie układamy naszą stertę tablic, aby utworzyć idealnie posortowaną tablicę w porządku rosnącym.
- Na koniec wypisujemy posortowaną tablicę na wyjściu.
Wynik:
Dane wyjściowe znajdują się poniżej.
Pokażę ci obrazową reprezentację wydarzeń:
- Wprowadzone dane są najpierw przedstawiane w postaci jednowymiarowej tablicy w następujący sposób.

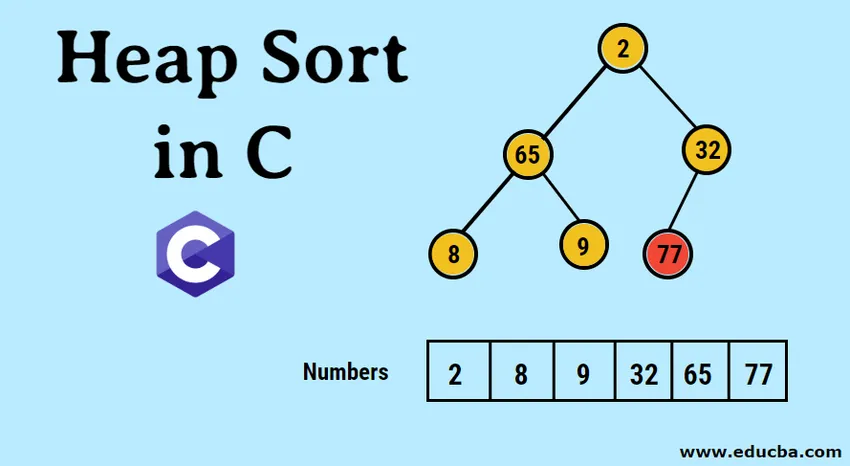
- Obrazowa reprezentacja utworzonego drzewa binarnego jest następująca:
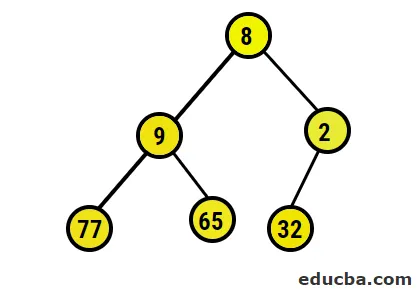
- Teraz przekonwertujemy na maksymalną stertę, upewniając się, że wszystkie węzły nadrzędne są zawsze większe niż węzły podrzędne. Jak wspomniano w danych wyjściowych pod tablicą posortowaną stosem, obrazową reprezentacją byłoby:
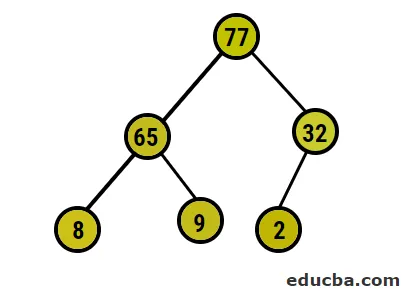
- Następnie zamienimy węzeł główny na skrajny węzeł liścia, a następnie usuniemy go z drzewa. Węzeł liścia byłby korzeniem od czasu do czasu tym samym procesem, w którym ponownie uzyskiwany jest najwyższy element w korzeniu
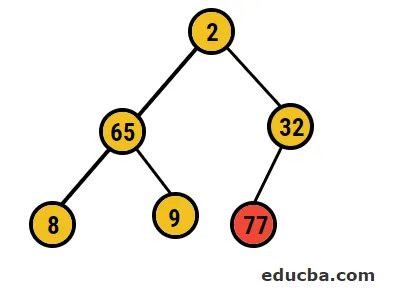
- Tak więc w tym przypadku 77 cyfr jest usuwanych z tego drzewa i umieszczanych w naszej posortowanej tablicy, a proces jest powtarzany.
Powyżej widzieliśmy to do tworzenia tablicy maksymalnej sterty. Ten sam proces dotyczy również formowania tablic stert min. Jak omówiono powyżej, jedyną różnicą jest związek między elementami nadrzędnymi i podrzędnymi.
Czy jako ćwiczenie możesz spróbować ułożyć sortowanie w malejącej kolejności?
Wniosek
Chociaż istnieje wiele technik sortowania, sortowanie sterty jest uważane za jedną z lepszych technik sortowania ze względu na złożoność czasu i przestrzeni. Złożoność czasowa dla wszystkich najlepszych, średnich i najgorszych przypadków wynosi O (nlogn), gdzie złożoność w najgorszym przypadku jest lepsza niż w najgorszym przypadku złożoność Quicksort, a złożoność przestrzeni wynosi O (1).
Polecane artykuły
Jest to przewodnik po sortowaniu sterty w C. Tutaj omawiamy logikę i kroki sortowania sterty z przykładowym kodem i danymi wyjściowymi wraz z reprezentacjami obrazkowymi. Możesz także zapoznać się z następującymi artykułami, aby dowiedzieć się więcej -
- Sortuj sterty w Javie
- Sortuj zaznaczenia w Javie
- Program Palindrome in C.
- Wzory w programowaniu C.
- Sortowanie sterty w C ++ (algorytm)
- Sortuj sterty w Pythonie
- Mnożenie macierzy programowania C.