
Wprowadzenie do funkcji w R.
Funkcja jest zdefiniowana jako zestaw instrukcji, służących do wykonania i wykonania dowolnego określonego zadania logicznego. Funkcja wykonuje pewne parametry wejściowe, które są znane jako argumenty do wykonania tego zadania. Funkcje pomagają w rozbiciu kodu na prostsze fragmenty poprzez logiczne uporządkowanie, co jest łatwiejsze do odczytania i zrozumienia. W tym temacie poznamy Funkcje w R.
Jak pisać funkcje w R?
Aby zapisać funkcję w R, oto składnia:
Fun_name <- function (argument) (
Function body
)
Tutaj można zobaczyć, że słowo R specyficzne dla „funkcji” jest używane do zdefiniowania dowolnej funkcji. Funkcja przyjmuje dane wejściowe w postaci argumentów. Ciało funkcji jest zestawem instrukcji logicznych, które są wykonywane na argumentach, a następnie zwraca dane wyjściowe. „Fun_name” to nazwa nadana funkcji, za pomocą której można ją wywołać w dowolnym miejscu w programie R.
Zobaczmy przykład, który będzie bardziej zrozumiały dla zrozumienia pojęcia funkcji w R.
Kod R.
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
wynik:
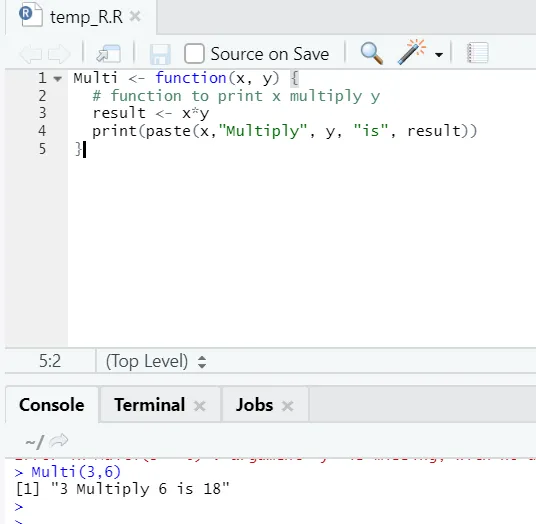
Tutaj stworzyliśmy nazwę funkcji „Multi”, która przyjmuje dwa argumenty jako dane wejściowe i zapewnia zwielokrotnione wyjście. Pierwszy argument to x, a drugi argument to y. Jak widać, wywołaliśmy funkcję o nazwie „Multi”. Tutaj, jeśli ktoś chce, argumenty można również ustawić na wartość domyślną.
Różne typy funkcji w R.
Różne funkcje R ze składnią i przykładami (wbudowane, matematyczne, statystyczne itp.)
1) Wbudowana funkcja -
Są to funkcje, które są dostarczane z R w celu rozwiązania określonego zadania poprzez przyjęcie argumentu jako danych wejściowych i podanie wyniku na podstawie danych wejściowych. Omówmy tutaj kilka ważnych ogólnych funkcji R:
a) Sortuj: Dane mogą być sortowane w kolejności rosnącej lub malejącej. Dane mogą określać, czy wektor zmiennej ciągłej czy zmienna czynnikowa.
Składnia:

Oto wyjaśnienie jego parametrów:
- x: Jest to wektor zmiennej ciągłej lub zmiennej czynnikowej
- malejące: Można ustawić Prawda / Fałsz, aby kontrolować kolejność rosnącą lub malejącą. Domyślnie jest to FALSE`.
- last: jeśli wektor ma wartości NA, należy go umieścić na końcu, czy nie
Kod R i dane wyjściowe:
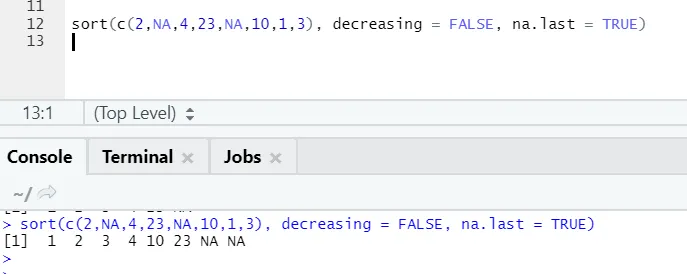
Tutaj można zauważyć, w jaki sposób wartości „NA” są wyrównane na końcu. Ponieważ nasz parametr na.last = True był prawdziwy.
b) Sekwencja : Generuje sekwencję liczby między dwiema określonymi liczbami.
Składnia
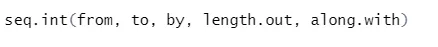
Oto wyjaśnienie jego parametrów:
- od, do początkowej i końcowej wartości sekwencji.
- przez: Zwiększenie / przerwa między dwiema kolejnymi liczbami w sekwencji
- length.out: wymagana długość sekwencji.
- Along.with: Odnosi się do długości od długości tego argumentu
Kod R i dane wyjściowe:
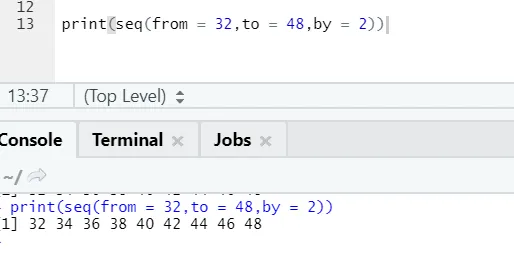
Tutaj można zauważyć, że generowana sekwencja ma inkrementację 2, ponieważ przez jest zdefiniowane jako 2.
c) Toupper, tolower: Dwie funkcje: toupper i tolower są funkcjami zastosowanymi na łańcuchu, aby zmienić wielkość liter w zdaniach.
Kod R i dane wyjściowe:
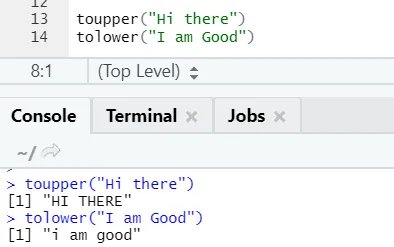
Można zauważyć, jak zmieniają się litery w przypadku zastosowania do funkcji.
d) Rnorm: Jest to wbudowana funkcja, która generuje losowe liczby.
Kod R i dane wyjściowe:
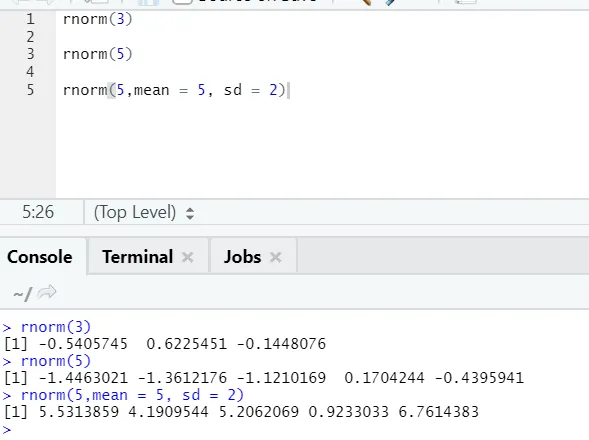
Funkcja rnorm przyjmuje pierwszy argument, który mówi, ile liczb należy wygenerować.
e) Rep: Ta funkcja replikuje wartość tyle razy, ile określono.
Składnia R: rnorm (x, n)
Tutaj x reprezentuje wartość do replikacji, a n reprezentuje liczbę powtórzeń.
Kod R i dane wyjściowe:
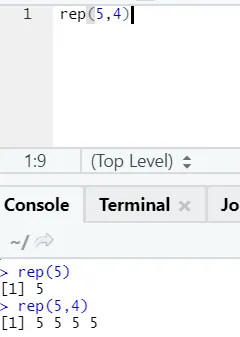
f) Wklej: Ta funkcja służy do łączenia ciągów znaków z określonym znakiem pomiędzy nimi.
składnia
paste(x, sep = “”, collapse = NULL)
Kod R.
paste("fish", "water", sep=" - ")
Wyjście R:
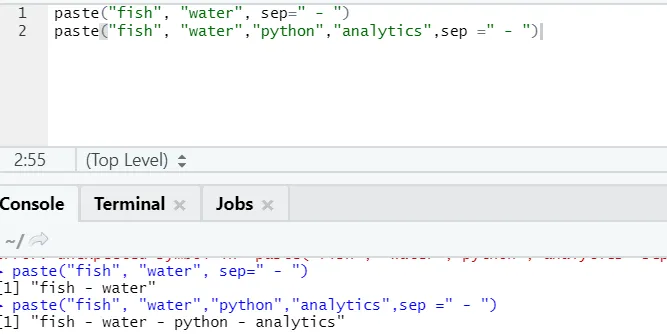
Jak widać, możemy również wkleić więcej niż dwa ciągi. Sep to ten konkretny znak, który dodaliśmy między łańcuchami. Domyślnie sep to spacja.
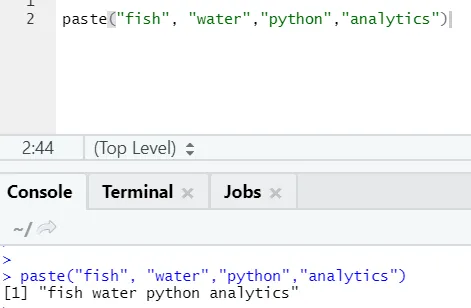
Istnieje jeszcze jedna podobna funkcja, o której wszyscy powinni wiedzieć, to paste0.
Funkcja paste0 (x, y, collapse) działa podobnie do funkcji paste (x, y, sep = „”, collapse)
Zobacz przykład poniżej:
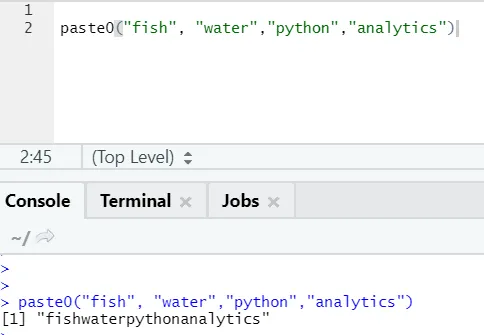
Krótko mówiąc, aby podsumować wklej i wklej0:
Paste0 jest szybszy niż pasta, jeśli chodzi o konkatenację łańcuchów bez żadnego separatora. Jak wklej zawsze szuka „sep” i domyślnie jest w nim spacja.
g) Strsplit: Ta funkcja służy do dzielenia łańcucha. Zobaczmy proste przypadki:
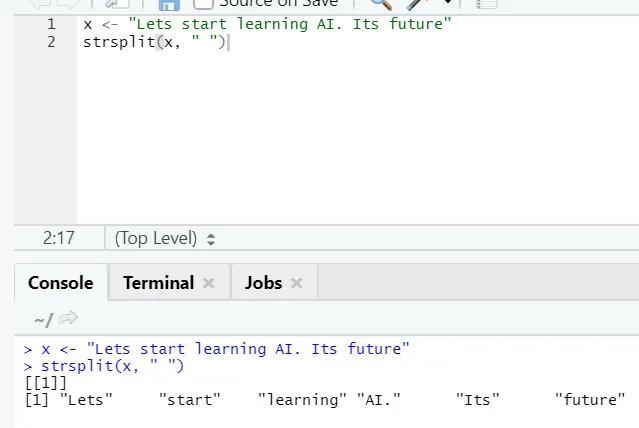
h) Rbind: Funkcja rbind pomaga w czesaniu wektorów o tej samej liczbie kolumn, jedna nad drugą.
Przykład
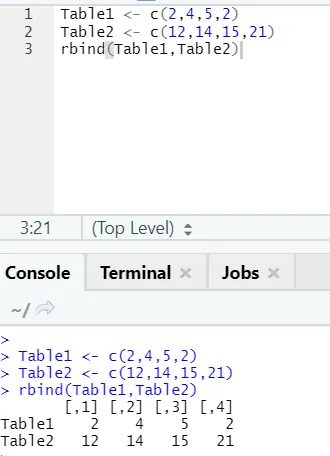
i) cbind: Łączy wektory o tej samej liczbie rzędów, obok siebie.
Przykład
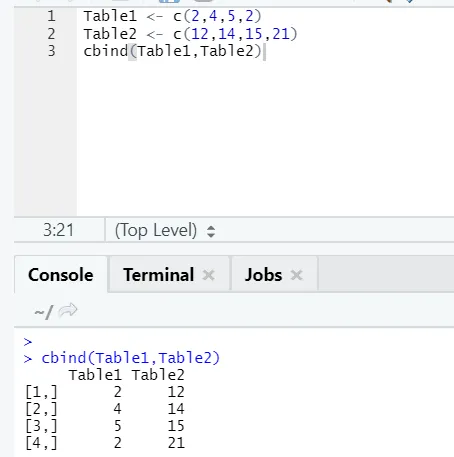
Jeśli liczba wierszy się nie zgadza, poniżej znajduje się błąd:

Zarówno cbind, jak i rbind pomaga w manipulacji danymi i ich przekształcaniu.
2) Funkcja matematyczna -
R zapewnia szeroki zakres funkcji matematycznych. Zobaczmy kilka z nich szczegółowo:
a) Sqrt: Ta funkcja oblicza pierwiastek kwadratowy z liczby lub wektora liczbowego.
Kod R i dane wyjściowe:
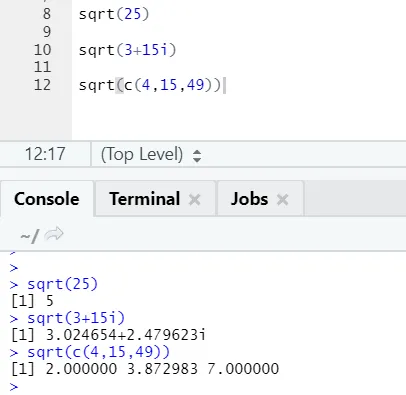
Można zobaczyć, jak obliczono pierwiastek kwadratowy z liczby, liczby zespolonej i sekwencji wektora numerycznego.
b) Exp: Ta funkcja oblicza wykładniczą wartość liczby lub wektora liczbowego.
Kod R i dane wyjściowe:
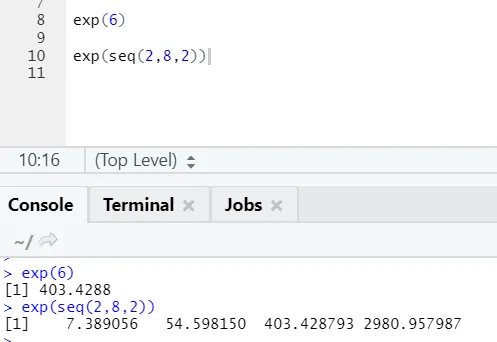
c) Cos, Sin, Tan: Są to funkcje trygonometryczne zaimplementowane tutaj w R.
Kod R i dane wyjściowe:
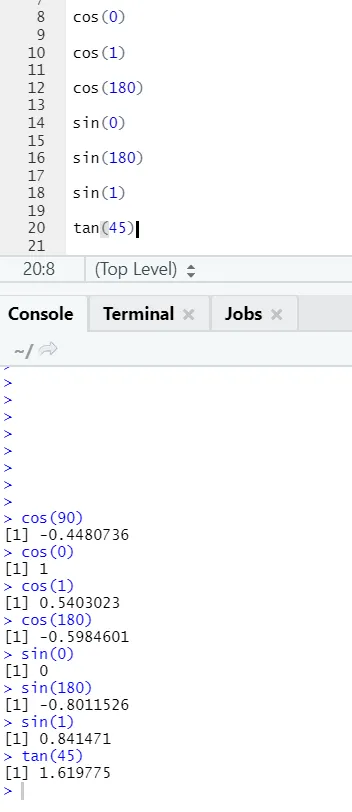
d) Abs: Ta funkcja zwraca bezwzględną wartość dodatnią liczby.
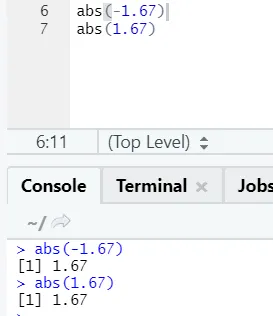
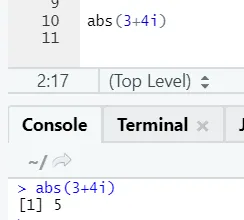
Jak widać, ujemna lub dodatnia liczby zostanie zwrócona w jej bezwzględnej formie. Zobaczmy to dla liczby zespolonej:
e) Dziennik: służy do znalezienia logarytmu liczby.
Oto przykład pokazany poniżej:
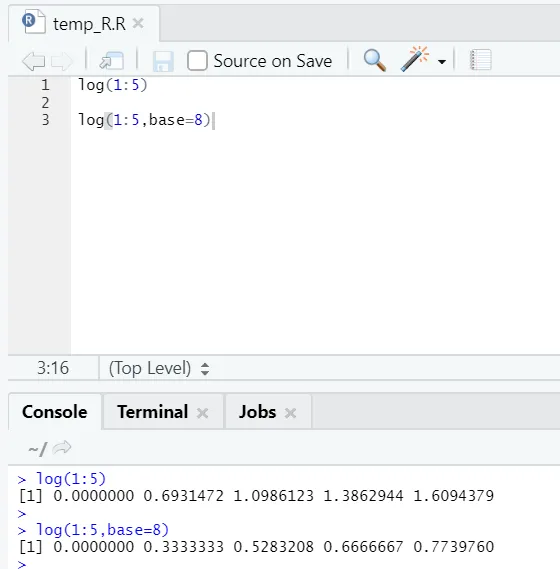
Tutaj można elastycznie zmieniać bazę, zgodnie z wymaganiami.
f) Cumsum: Jest to funkcja matematyczna, która daje sumy sumaryczne. Oto przykład poniżej:
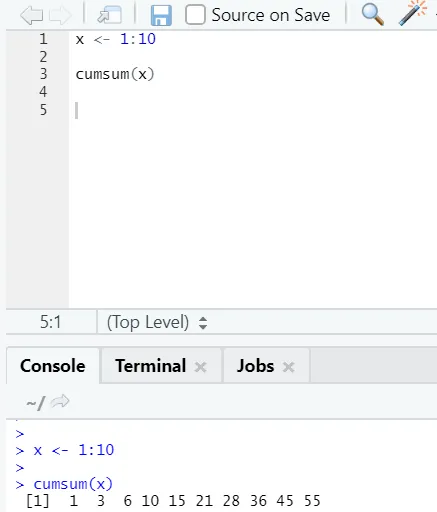
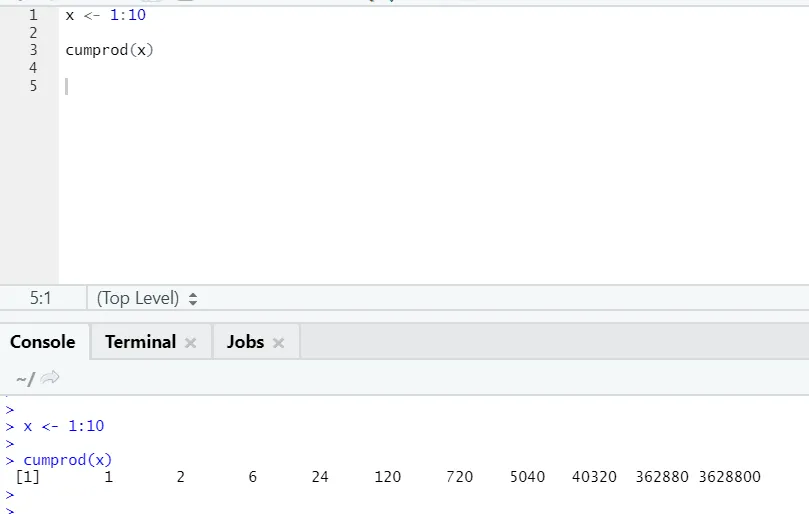
g) Cumprod: Podobnie jak funkcja matematyczna Cumsum, mamy cumprod, w którym występuje kumulacja mnożenia.
Zobacz przykład poniżej:
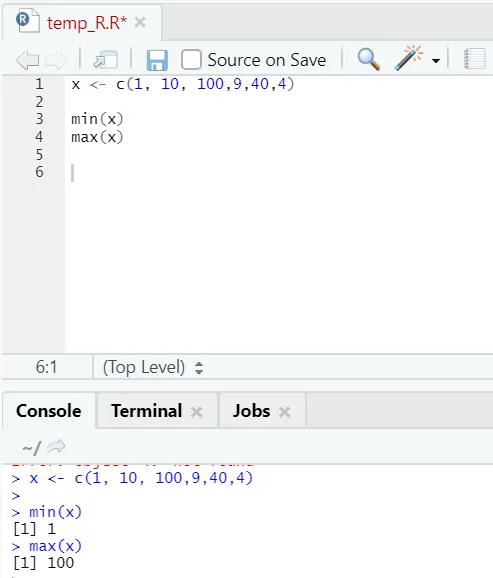
h) Max, Min: Pomoże Ci to znaleźć maksymalną / minimalną wartość w zestawie liczb. Zobacz poniżej związane z tym przykłady:
i) Pułap: Pułap jest funkcją matematyczną zwracającą najmniejszą liczbę całkowitą wyższą niż określona.
Spójrzmy na przykład:
sufit (2, 67)
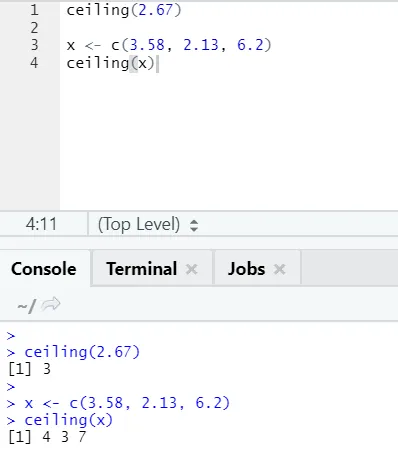
Jak można zauważyć, pułap jest nakładany zarówno na liczbę, jak i na listę, a wynik jest najmniejszą z następnej wyższej liczby całkowitej.
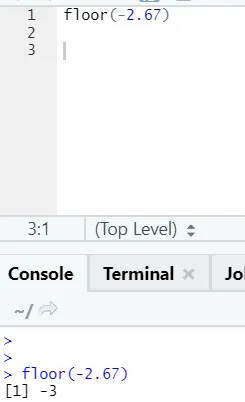
j) Piętro: Piętro to funkcja matematyczna zwraca najmniejszą liczbę całkowitą z podanej liczby.
Poniższy przykład pomoże ci lepiej to zrozumieć:
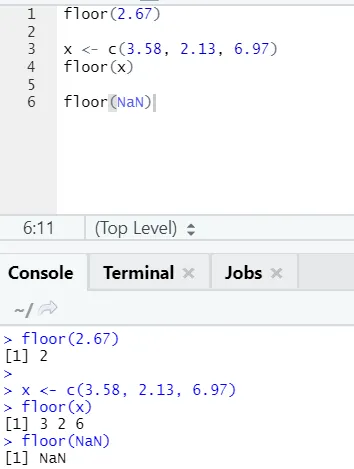
Działa to w ten sam sposób również w przypadku wartości ujemnych. Proszę spójrz:
3) Funkcje statystyczne -
Są to funkcje opisujące związany rozkład prawdopodobieństwa.
a) Mediana: Obliczono medianę z ciągu liczb.
Składnia
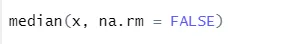
Kod R i dane wyjściowe:
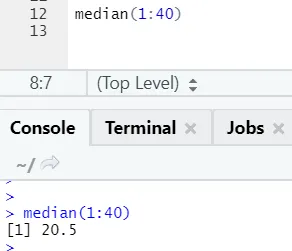
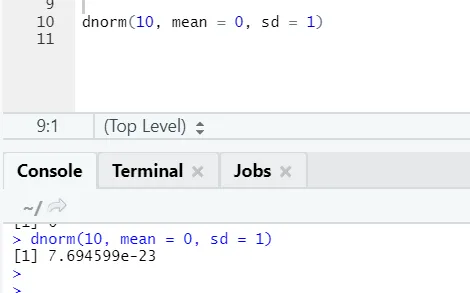
b) Dnorm: Odnosi się do rozkładu normalnego. Funkcja dnorm zwraca wartość funkcji gęstości prawdopodobieństwa dla rozkładu normalnego dla podanych parametrów dla x, μ i σ.
Kod R i dane wyjściowe:
c) Cov: Kowariancja mówi, czy dwa wektory są dodatnio, ujemnie lub całkowicie niezwiązane.
Kod R.
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Wyjście R:
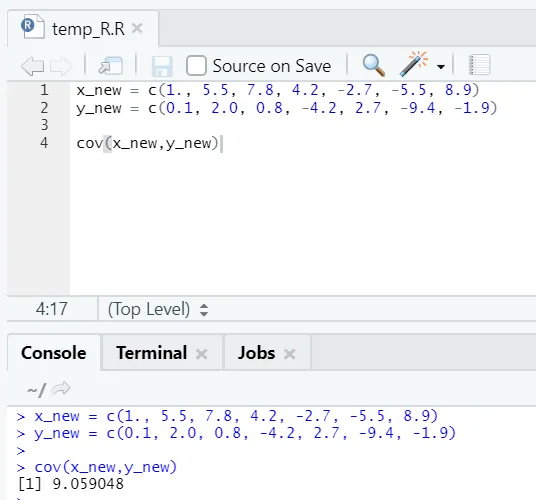
Jak widać, dwa wektory są dodatnio powiązane, co oznacza, że oba wektory poruszają się w tym samym kierunku. Jeśli kowariancja jest ujemna, oznacza to, że xiy są odwrotnie powiązane i dlatego poruszają się w przeciwnym kierunku.
d) Cor: Jest to funkcja znajdująca korelację między wektorami. W rzeczywistości podaje współczynnik asocjacji między dwoma wektorami, który jest znany jako „współczynnik korelacji”. Korelacja dodaje czynnik stopnia do kowariancji. Jeśli dwa wektory są dodatnio skorelowane, korelacja powie ci również, w jakim stopniu są one dodatnio powiązane.
Te trzy typy metod, których można użyć do znalezienia korelacji między dwoma wektorami:
- Korelacja Pearsona
- Korelacja Kendalla
- Korelacja Spearmana
W prostym formacie R wygląda to tak:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Tutaj xiy są wektorami.
Zobaczmy praktyczny przykład korelacji nad wbudowanym zestawem danych.
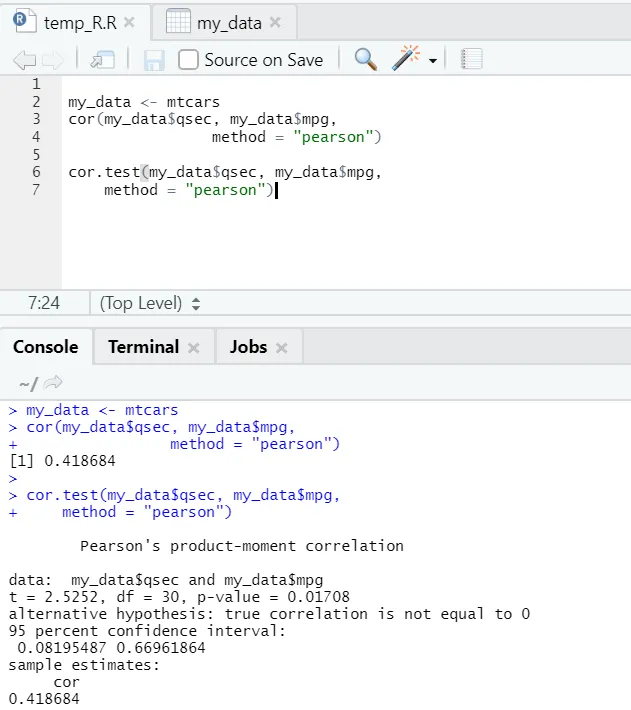
Widzimy więc, że funkcja „cor ()” podała współczynnik korelacji 0, 41 między „qsec” a „mpg”. Zaprezentowano jednak jeszcze jedną funkcję, tj. „Cor.test ()”, która nie tylko informuje o współczynniku korelacji, ale także o wartości p i związanej z nim wartości t. Interpretacja staje się znacznie łatwiejsza dzięki funkcji cor.test.
Podobnie można zrobić w przypadku dwóch pozostałych metod korelacji:
Kod R dla metody Pearsona:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Kod R dla metody Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Kod R dla metody Spearmana:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Współczynnik korelacji wynosi od -1 do 1.
Jeśli współczynnik korelacji jest ujemny, oznacza to, że gdy x zwiększa y maleje.
Jeśli współczynnik korelacji wynosi zero, oznacza to, że nie istnieje powiązanie między xiy.
Jeśli współczynnik korelacji jest dodatni, oznacza to, że gdy x wzrasta, y również ma tendencję do wzrostu.
e) Test T: Test T pokaże, czy dwa zestawy danych pochodzą z tych samych (zakładając) rozkładów normalnych, czy nie.
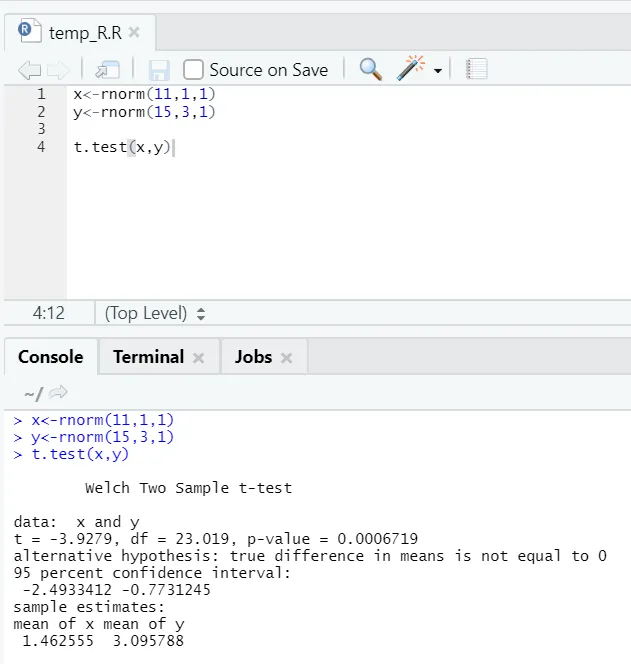
W tym miejscu powinieneś odrzucić hipotezę zerową, że dwie średnie są równe, ponieważ wartość p jest mniejsza niż 0, 05.
Ta pokazana instancja jest typu: niesparowane zestawy danych z nierównymi wariancjami. Podobnie można wypróbować ze sparowanym zestawem danych.
f) Prosta regresja liniowa: Pokazuje zależność między predyktorem / zmienną niezależną a odpowiedzią / zmienną zależną.
Prostym praktycznym przykładem może być przewidywanie masy ciała osoby, jeśli wysokość jest znana.
Składnia R.
lm(formula, data)
Tutaj formuła przedstawia zależność między danymi wyjściowymi tj. Y a zmienną wejściową iex. Dane reprezentują zestaw danych, do którego należy zastosować formułę.
Zobaczmy jeden praktyczny przykład, w którym powierzchnia podłogi jest zmienną wejściową, a czynsz jest zmienną wyjściową.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
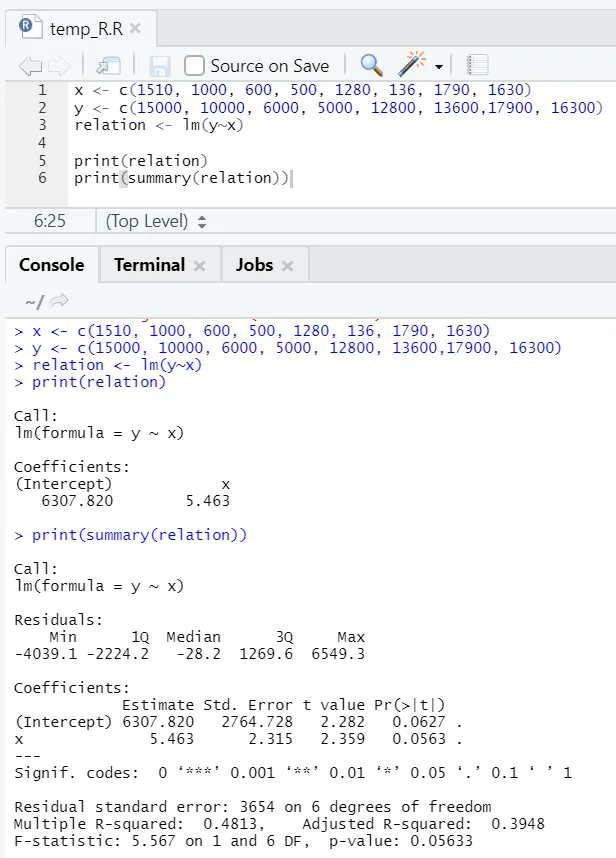
Tutaj wartość P jest nie mniejsza niż 5%. Dlatego nie można odrzucić hipotezy zerowej. Nie ma większego znaczenia, aby udowodnić związek między powierzchnią podłogi a czynszem.
Tutaj wartość R-kwadrat wynosi 0, 4813. Oznacza to, że tylko 48% wariancji zmiennej wyjściowej można wyjaśnić zmienną wejściową.
Powiedzmy, że teraz musimy przewidzieć wartość powierzchni podłogi na podstawie wyżej dopasowanego modelu.
Kod R.
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Wyjście R:
Po wykonaniu powyższego kodu R dane wyjściowe będą wyglądać następująco:
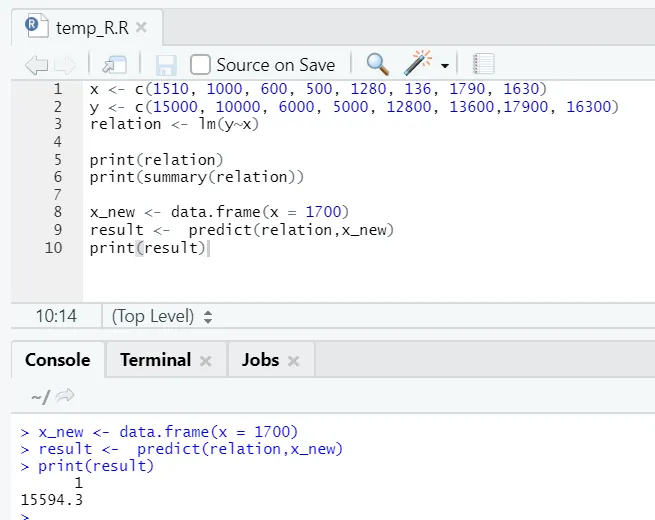
Można dopasować i wizualizować regresję. Oto kod R dla tego:
# Nadaj nazwę plikowi wykresu png.
png(file = "LinearRegressionSample.png.webp")
# Wykreśl wykres.
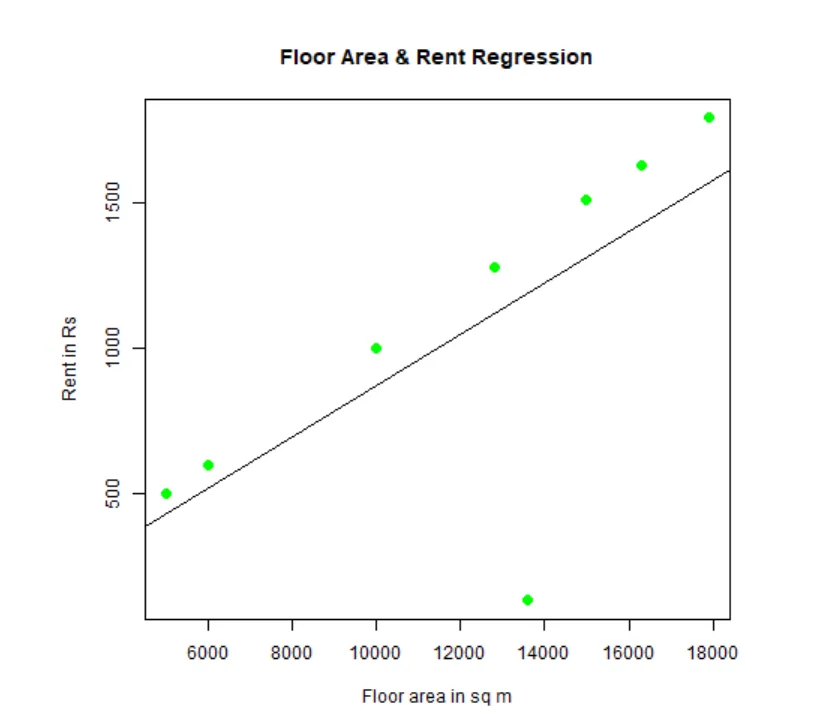
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Zapisz plik.
dev.off()
Ten wykres „LinearRegressionSample.png.webp” zostanie wygenerowany w bieżącym katalogu roboczym.
g) Test chi-kwadrat
Jest to funkcja statystyczna w R. Ten test ma znaczenie w celu udowodnienia, czy istnieje korelacja między dwiema zmiennymi kategorialnymi.
Ten test działa również tak, jak inne testy statystyczne oparte na wartości p, można zaakceptować lub odrzucić hipotezę zerową.
Składnia R.
chisq.test(data), /code>
Zobaczmy jeden praktyczny przykład tego.
Kod R.
# Załaduj bibliotekę.
library(datasets)
data(iris)
# Utwórz ramkę danych z głównego zestawu danych.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Utwórz tabelę z potrzebnymi zmiennymi.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Wykonaj test Chi-Square.
print(chisq.test(iris.data))
Wyjście R:
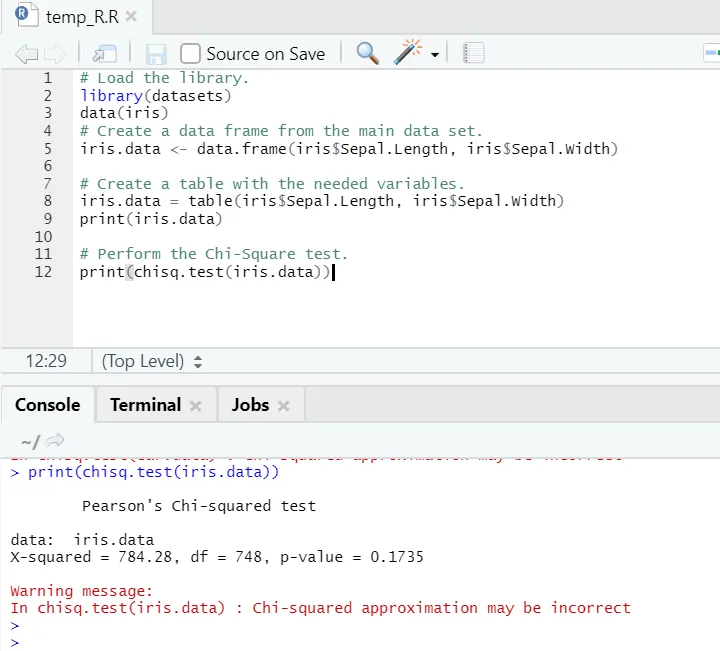
Jak widać, test chi-kwadrat został przeprowadzony na zestawie danych tęczówki, biorąc pod uwagę jego dwie zmienne „Sepal. Długość ”i„ Sepal.Width ”.
Wartość p jest nie mniejsza niż 0, 05, stąd nie istnieje korelacja między tymi dwiema zmiennymi. Lub możemy powiedzieć, że te dwie zmienne nie są od siebie zależne.
Wniosek
Funkcje w R są proste, łatwe do dopasowania, łatwe do uchwycenia, a jednocześnie bardzo wydajne. Widzieliśmy różnorodność funkcji, które są używane jako część podstaw w R. Kiedy już zaznajomisz się z tymi funkcjami omówionymi powyżej, możesz eksplorować inne odmiany funkcji. Funkcje pomagają, sprawiając, że kod działa w prosty i zwięzły sposób. Funkcje mogą być wbudowane lub zdefiniowane przez użytkownika, wszystko zależy od potrzeby rozwiązania problemu. Funkcje nadają programowi dobry kształt.
Polecane artykuły
To jest przewodnik po funkcjach w R. tutaj omawiamy, jak pisać funkcje w R i różne typy funkcji w R ze składnią i przykładami. Możesz także spojrzeć na następujący artykuł, aby dowiedzieć się więcej -
- Funkcje ciągów R.
- Funkcje ciągów SQL
- Funkcje ciągów T-SQL
- Funkcje ciągu PostgreSQL