
Formuła marginesu błędu (spis treści)
- Formuła marginesu błędu
- Przykłady formuły marginesu błędu (z szablonem Excel)
- Kalkulator marginesu błędu
Formuła marginesu błędu
W statystyce obliczamy przedział ufności, aby zobaczyć, gdzie spadnie wartość danych z przykładowej statystyki. Zakres wartości poniżej i powyżej statystyki próbki w przedziale ufności jest znany jako Margines błędu. Innymi słowy, jest to w zasadzie stopień błędu w statystyce próbki. Im wyższy margines błędu, tym mniejsze zaufanie do wyników, ponieważ stopień odchylenia w tych wynikach jest bardzo wysoki. Jak sama nazwa wskazuje, margines błędu to zakres wartości powyżej i poniżej rzeczywistych wyników. Na przykład, jeśli otrzymamy odpowiedź w ankiecie, w której 70% osób odpowiedziało „dobrze”, a margines błędu wynosi 5%, oznacza to, że ogólnie od 65% do 75% populacji uważa, że odpowiedź jest „dobra” .
Wzór na margines błędu -
Margin of Error = Z * S / √n
Gdzie:
- Z - Z score
- S - Odchylenie standardowe populacji
- n - Rozmiar próbki
Inną formułą obliczania marginesu błędu jest:
Margin of Error = Z * √((p * (1 – p)) / n)
Gdzie:
- p - proporcja próbki (część próbki, która jest sukcesem)
Teraz, aby znaleźć pożądany wynik Z, musisz znać przedział ufności próbki, ponieważ wynik Z zależy od tego. Poniższa tabela zawiera stosunek przedziału ufności do wyniku Z:
| Przedział ufności | Z - wynik |
| 80% | 1, 28 |
| 85% | 1.44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Po poznaniu przedziału ufności możesz użyć odpowiedniej wartości z i stamtąd obliczyć margines błędu.
Przykłady formuły marginesu błędu (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie marginesu błędu.
Możesz pobrać ten szablon marginesu błędu tutaj - szablon marginesu błęduWzór marginesu błędu - przykład nr 1
Powiedzmy, że przeprowadzamy ankietę, aby sprawdzić, jaki wynik oceniają studenci. Wybraliśmy losowo 500 studentów i poprosiliśmy o ocenę. Średnia to 2, 4 na 4, a odchylenie standardowe to na przykład 30%. Załóżmy, że przedział ufności wynosi 99%. Oblicz margines błędu.
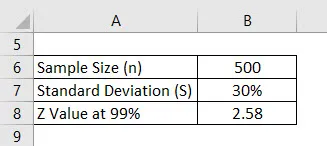
Rozwiązanie:
Margines błędu jest obliczany przy użyciu poniższego wzoru
Margines błędu = Z * S / √n
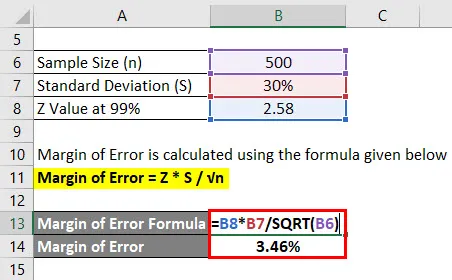
- Margines błędu = 2, 58 * 30% / √ (500)
- Margines błędu = 3, 46%
Oznacza to, że przy 99% ufności średnia ocena uczniów wynosi 2, 4 plus lub minus 3, 46%.
Wzór na margines błędu - przykład 2
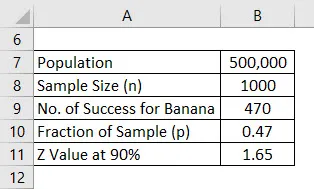
Powiedzmy, że wprowadzasz na rynek nowy produkt zdrowotny, ale nie wiesz, jaki smak spodoba się ludziom. Jesteś zdezorientowany między smakiem banana i wanilii i postanowiłeś przeprowadzić ankietę. Twoja populacja to 500 000, co jest twoim rynkiem docelowym, i dlatego zdecydowałeś się zapytać o opinię 1000 osób, a to zrobi próbkę. Załóżmy, że przedział ufności wynosi 90%. Oblicz margines błędu.
Rozwiązanie:
Po zakończeniu ankiety dowiedziałeś się, że 470 osobom smakuje banan, a 530 poprosiło o smak waniliowy.
Margines błędu jest obliczany przy użyciu poniższego wzoru
Margines błędu = Z * √ ((p * (1 - p)) / n)
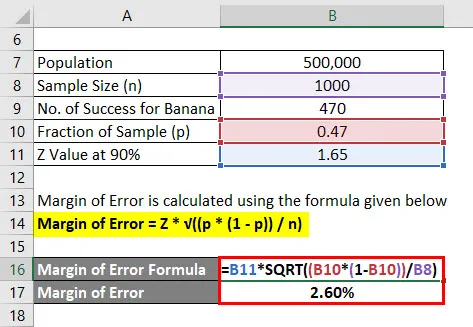
- Margines błędu = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Margines błędu = 2, 60%
Możemy więc powiedzieć, że z 90% pewnością, że 47% wszystkich osób lubiło smak bananów plus minus 2, 60%.
Wyjaśnienie
Jak omówiono powyżej, margines błędu pomaga nam zrozumieć, czy wielkość próby Twojej ankiety jest odpowiednia, czy nie. W przypadku, gdy błąd marginesu jest zbyt duży, może się zdarzyć, że nasza próba jest zbyt mała i musimy ją zwiększyć, aby wyniki próby były lepiej dopasowane do wyników populacji.
Istnieje kilka scenariuszy, w których margines błędu nie będzie przydatny i nie pomoże nam w śledzeniu błędu:
- Jeśli pytania ankiety nie są zaprojektowane i nie pomagają uzyskać wymaganej odpowiedzi
- Jeśli osoby, które odpowiadają na ankietę, mają pewne uprzedzenia dotyczące produktu, dla którego przeprowadzana jest ankieta, wynik również nie jest zbyt dokładny
- Jeśli wybrana próbka jest właściwym przedstawicielem populacji, również w takim przypadku wyniki będą dalekie.
Ponadto jednym dużym założeniem jest to, że populacja jest normalnie rozmieszczona. Jeśli więc wielkość próby jest zbyt mała, a rozkład populacji nie jest normalny, wyniku z nie można obliczyć i nie będziemy w stanie znaleźć marginesu błędu.
Trafność i zastosowania wzoru marginesu błędu
Ilekroć używamy danych przykładowych w celu znalezienia odpowiedniej odpowiedzi dla zestawu populacji, istnieje niepewność i prawdopodobieństwo, że wynik może odbiegać od rzeczywistego wyniku. Margines błędu powie nam, że jaki jest poziom odchylenia, istnieje próbka wyjściowa. Musimy zminimalizować margines błędu, aby nasze próbki przedstawiły rzeczywistą historię danych dotyczących populacji. Więc obniż margines błędu, lepsze będą wyniki. Margines błędu uzupełnia i uzupełnia posiadane przez nas informacje statystyczne. Na przykład, jeśli z ankiety wynika, że 48% ludzi woli spędzać czas w domu w weekend, nie możemy być tak precyzyjni i brakuje pewnych elementów w tych informacjach. Kiedy wprowadzimy tutaj margines błędu, powiedzmy 5%, wynik zostanie zinterpretowany jako 43-53% osób lubiło być w domu w weekend, co jest całkowicie sensowne.
Kalkulator marginesu błędu
Możesz użyć następującego kalkulatora marginesu błędu
| Z | |
| S. | |
| .N | |
| Margines błędu | |
| Margines błędu | = |
|
|
Polecane artykuły
Jest to przewodnik po formule Margines błędu. Tutaj omawiamy sposób obliczania marginesu błędu wraz z praktycznymi przykładami. Zapewniamy również kalkulator marginesu błędu z szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przewodnik po formule amortyzacji po linii prostej
- Przykłady wzoru czasu podwojenia
- Jak obliczyć amortyzację?
- Wzór na twierdzenie o granicy centralnej
- Wynik Altman Z | Definicja | Przykłady
- Formuła amortyzacji | Przykłady z szablonem Excel