
Formuła punktacji Z (spis treści)
- Formuła
- Przykłady
- Kalkulator
Co to jest formuła Z Score?
„Wynik Z” jest jednym z najczęściej używanych narzędzi statystycznych, które stosuje się do standaryzacji wyniku, pod warunkiem, że znane są średnie populacji i odchylenie standardowe. W związku z tym wynik Z jest również znany jako wynik standardowy. Wynik Z zmienia się w zakresie od -3-krotności odchylenia standardowego do +3-krotności odchylenia standardowego ze średnią zero i odchyleniem standardowym jeden. Wzór na wynik Z zmiennej można uzyskać przez odjęcie średniej populacji od danej zmiennej (która jest częścią zbioru danych lub populacji), a następnie podzielenie wyniku przez odchylenie standardowe populacji. Matematycznie jest reprezentowany jako
Z = (X – μ) / σ
gdzie,
- X = Zmienna z populacji
- μ = średnia populacji
- σ = odchylenie standardowe populacji
Przykłady wzoru Z Score (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczanie wyniku Z.
Możesz pobrać ten szablon Excel Formula Formula Z tutaj - szablon Excel Formula Z ScoreFormuła Z score - przykład nr 1
Weźmy przykład Manny'ego, który niedawno pojawił się na SAT. Udało mu się zdobyć 1109 w tej próbie. Jednak zgodnie z dostępnymi informacjami średni wynik dla SAT pozostał około 1030 z odchyleniem standardowym wynoszącym 250. Oblicz wynik Z dla wyniku SAT Manny'ego i oceń, jak dobrze sobie poradził w porównaniu do przeciętnych uczestników testu.
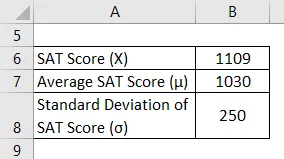
Rozwiązanie:
Z Wynik jest obliczany przy użyciu poniższego wzoru
Z = (X - μ) / σ
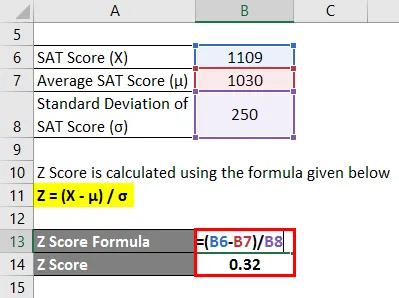
- Wynik Z = (1109 - 1030) / 250
- Wynik Z = 0, 32
W związku z tym wynik SAT Manny'ego jest o 0, 32 odchylenia standardowego wyższy niż średni wynik uczestników testu, co wskazuje, że 62, 55% uczestników testu uzyskało mniej niż Manny.
Wzór na wynik Z - przykład 2
Weźmy teraz przykład Chelsea, która dwukrotnie napisała SAT i chce porównać w niej swoje wyniki. Udało jej się zdobyć 1085 i 1059 odpowiednio w pierwszej i drugiej próbie. Zgodnie z dostępnymi informacjami średni wynik i odchylenie standardowe podczas pierwszej próby wyniosły odpowiednio 1100 i 230, podczas gdy w tej drugiej odpowiednio 1050 i 240. Pomóż Chelsea zdecydować, w którym egzaminie wypadła lepiej.
Rozwiązanie:
1 próba
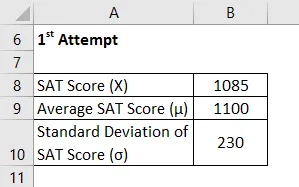
Z Wynik jest obliczany przy użyciu poniższego wzoru
Z = (X - μ) / σ
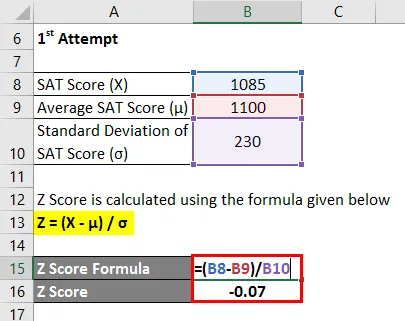
- Wynik Z = (1085–1100) / 230
- Wynik Z = -0, 07
W związku z tym wynik SAT Chelsea w pierwszej próbie jest o 0, 07 odchylenia standardowego niższy niż średni wynik osób wykonujących test, co wskazuje, że 47, 40% osób wykonujących test uzyskało mniej niż Chelsea podczas pierwszej próby.
2. próba
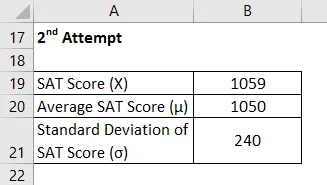
Z Wynik jest obliczany przy użyciu poniższego wzoru
Z = (X - μ) / σ
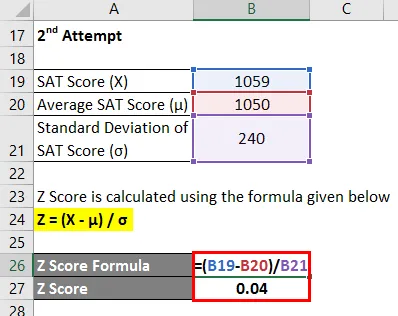
- Wynik Z = (1059–1050) / 240
- Wynik Z = 0, 04
W związku z tym wynik SAT Chelsea w drugiej próbie jest o 0, 04 odchylenia standardowego wyższy niż średni wynik osób wykonujących test, co wskazuje, że 51, 50% osób wykonujących test uzyskało mniej niż Chelsea podczas drugiej próby.
Tak więc z porównania wyników Z widać, że Chelsea osiągnęła lepsze wyniki podczas drugiej próby.
Wyjaśnienie
Wzór na wynik Z można uzyskać, wykonując następujące kroki:
Krok 1: Po pierwsze, zbuduj populację z dużą liczbą zmiennych, a zmienne są oznaczone Xi.
Krok 2: Następnie obliczana jest liczba zmiennych w populacji i oznaczana jest przez N.
Krok 3: Następnie oblicza się średnią populacji, sumując wszystkie zmienne, a następnie dzieląc przez całkowitą liczbę zmiennych (krok 2) w zbiorze danych. Średnia populacji jest oznaczona przez μ.
μ = ∑ X i / N
Krok 4: Następnie odejmij średnią z każdej zmiennej zestawu danych, aby obliczyć ich odchylenie od średniej.
tj. (X i - μ) to odchylenie dla i- tego punktu danych.
Krok 5: Następnie oblicz kwadratowe odchylenia dla zmiennych, tj. (X i - μ) 2 .
Krok 6: Następnie dodaj wszystkie kwadratowe odchylenia, a następnie podziel sumę przez liczbę zmiennych w zbiorze danych, aby uzyskać wariancję.
σ 2 = ∑ (X i - μ) 2 / N
Krok 7: Następnie standardowe odchylenie populacji oblicza się, obliczając pierwiastek kwadratowy wariancji obliczonej w powyższym kroku.
σ = √ ∑ (X i - μ) 2 / N
Krok 8: W końcu wzór na wynik Z oblicza się przez odjęcie średniej populacji (krok 3) od zmiennej, a następnie podzielenie wyniku przez odchylenie standardowe populacji (krok 7), jak pokazano poniżej.
Z = (X - μ) / σ
Trafność i zastosowania wzoru Z Score
Z punktu widzenia statystyki koncepcja wyniku Z jest bardzo ważna, ponieważ jest przydatna w określaniu prawdopodobieństwa wystąpienia zdarzenia w rozkładzie normalnym. W rzeczywistości wynik Z jest także wykorzystywany do porównywania dwóch wyników surowych z dwóch różnych rozkładów normalnych i odbywa się to poprzez konwersję wyników surowych na wynik Z lub wynik standardowy. Ponadto dodatni wynik Z implikuje wynik wyższy niż średnia, podczas gdy ujemny wynik Z implikuje wynik mniejszy niż średnia.
Kalkulator formuły Z Score
Możesz użyć następującego kalkulatora Z Score Formula
| X | |
| µ | |
| σ | |
| Z | |
| Z = |
|
|
Polecane artykuły
To był przewodnik po Formule Z Score. Tutaj omawiamy sposób obliczania wyniku Z wraz z praktycznymi przykładami. Oferujemy również kalkulator Z Score z szablonem Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przykłady wzoru wielkości próbki
- Jak obliczyć średnią ważoną?
- Kalkulator formuły korelacji
- Wzór do obliczenia rozkładu normalnego
- Przykłady wyniku Altmana Z.