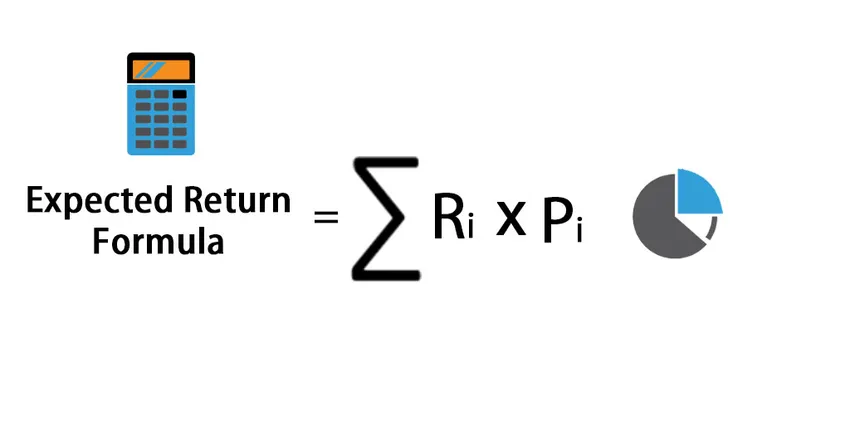
Formuła oczekiwanego zwrotu (spis treści)
- Formuła oczekiwanego zwrotu
- Przykłady formuły oczekiwanego zwrotu (z szablonem Excel)
- Kalkulator formuły oczekiwanego zwrotu
Formuła oczekiwanego zwrotu
Oczekiwany zwrot może być zdefiniowany jako prawdopodobny zwrot dla portfela posiadanego przez inwestorów na podstawie przeszłych zwrotów lub może być również zdefiniowany jako oczekiwana wartość portfela na podstawie rozkładu prawdopodobieństwa prawdopodobnych zwrotów.
Oto formuła oczekiwanego zwrotu -
Expected Return = Expected Return=∑ (R i * P i )
Gdzie
- R i - Oczekiwanie na zwrot każdego scenariusza
- P i - Prawdopodobieństwo zwrotu w tym scenariuszu
- i - Możliwe scenariusze od 1 do n
Przykłady formuły oczekiwanego zwrotu (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć sposób obliczania formuły oczekiwanego zwrotu.
Formuła oczekiwanego zwrotu - przykład nr 1
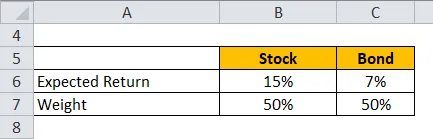
Weźmy przykład portfela akcji i obligacji, w których akcje mają 50% wagi, a obligacje 50%. Oczekiwany zwrot akcji wynosi 15%, a oczekiwany zwrot z obligacji 7%.
Oczekiwany zwrot oblicza się według wzoru podanego poniżej
Oczekiwany zwrot z portfela = waga akcji * Oczekiwany zwrot z akcji + waga obligacji * Oczekiwany zwrot z obligacji
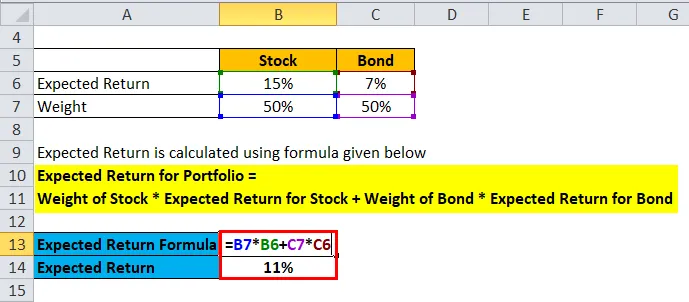
- Oczekiwany zwrot z portfela = 50% * 15% + 50% * 7%
- Oczekiwany zwrot z portfela = 7, 5% + 3, 5%
- Oczekiwany zwrot z portfela = 11%
Formuła oczekiwanego zwrotu - przykład 2
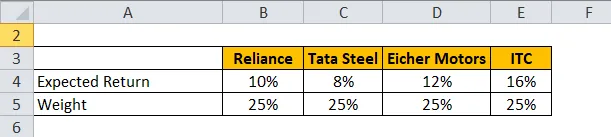
Weźmy przykład portfela, który ma akcje Reliance, Tata Steel, Eicher Motors i ITC.
Oczekiwany zwrot oblicza się według wzoru podanego poniżej
Oczekiwany zwrot dla portfela = ∑ Waga każdego zapasu * Oczekiwany zwrot dla każdego zapasu

- Oczekiwany zwrot z portfela = 25% * 10% + 25% * 8% + 25% * 12% + 25% * 16%
- Oczekiwany zwrot z portfela = 2, 5% + 2% + 3% + 4%
- Oczekiwany zwrot z portfela = 11, 5%
Formuła oczekiwanego zwrotu - przykład 3
Weźmy przykład portfela HUL, HDFC i 10-letnich obligacji rządowych.
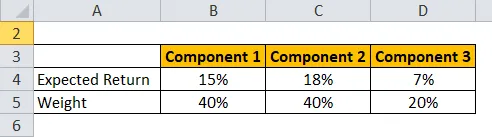
Oczekiwany zwrot oblicza się według wzoru podanego poniżej
Oczekiwany zwrot dla portfela = ∑ Waga każdego komponentu * Oczekiwany zwrot dla każdego komponentu
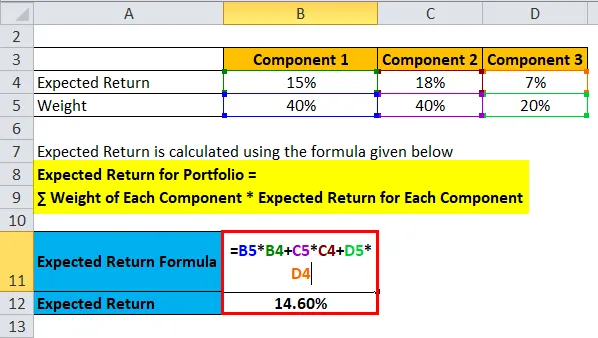
- Oczekiwany zwrot z portfela = 40% * 15% + 40% * 18% + 20% * 7%
- Oczekiwany zwrot z portfela = 6% + 7, 2% + 1, 40%
- Oczekiwany zwrot z portfela = 14, 60%
Możesz pobrać ten szablon Excel Formuła oczekiwanego zwrotu - Excel Formuła oczekiwanego zwrotu
Wyjaśnienie formuły oczekiwanego zwrotu
Oczekiwany zwrot może być zdefiniowany jako prawdopodobny zwrot dla portfela posiadanego przez inwestorów na podstawie przeszłych zwrotów lub może być również zdefiniowany jako oczekiwana wartość portfela na podstawie rozkładu prawdopodobieństwa prawdopodobnych zwrotów. Oczekiwany zwrot można rozpatrywać w perspektywie krótkoterminowej jako zmienną losową, która może przyjmować różne wartości w oparciu o pewne wyraźne prawdopodobieństwa. Ta losowa zmienna ma wartości z określonego zakresu i może przyjmować wartości tylko z tego określonego zakresu. Dlatego obliczenie oczekiwanego zwrotu opiera się na danych historycznych i dlatego może nie być wiarygodne w prognozowaniu przyszłych zwrotów. Można to postrzegać jako miarę różnych prawdopodobieństw i prawdopodobieństwa uzyskania dodatniego zwrotu z inwestycji oraz wartości tego zwrotu.
Ma to na celu dać inwestorowi wyobrażenie o innym poziomie ryzyka, jakie są różne scenariusze z różnymi prawdopodobieństwami, które przyniosą możliwy zwrot większy niż zwrot wolny od ryzyka. Jak wszyscy wiemy, zwrotem bez ryzyka byłaby rentowność 10-letnich obligacji skarbowych rządu Stanów Zjednoczonych.
Trafność i zastosowania formuły oczekiwanego zwrotu
Jak wspomniano powyżej, obliczenie oczekiwanego zwrotu opiera się na danych historycznych, a zatem ma ograniczenia w prognozowaniu przyszłych możliwych zwrotów. Inwestorzy muszą pamiętać o różnych innych czynnikach i nie inwestować w oparciu o obliczony oczekiwany zwrot. Biorąc przykład:
Portfolio A - 10%, 12%, -9%, 2%, 25%
Portfolio B - 9%, 7%, 6%, 6%, 12%
Jeśli weźmiemy pod uwagę oba powyższe portfele, oba mają oczekiwany zwrot w wysokości 8%, ale portfel A wykazuje duże ryzyko z powodu dużej zmienności zwrotów. Dlatego inwestorzy muszą wziąć pod uwagę to ryzyko, które jest obliczane za pomocą miar takich jak odchylenie standardowe i wariancja.
- Wariancja - może być zdefiniowana jako odmiana zestawu punktów danych wokół ich średniej wartości. Jest on obliczany na podstawie średniej ważonej prawdopodobieństwem kwadratowych odchyleń od średniej. Jest to miara ryzyka, którą inwestorzy muszą wziąć pod uwagę.
Najpierw należy obliczyć średnią wszystkich zwrotów. Następnie odchylenie każdego zwrotu jest wykrywane z wartości głównej i podnoszone do kwadratu, aby zapewnić wszystkie pozytywne wyniki. A kiedy zostaną podniesione do kwadratu, są mnożone przez odpowiednie wartości prawdopodobieństwa, aby znaleźć wariancję.
Odchylenie portfela można obliczyć na podstawie następującego wzoru: - Jeśli istnieją dwa portfele A i B
Odchylenie portfela = w A 2 * σ A 2 + w B 2 * σ B 2 + 2 * w A * w B * Cov (A, B)
Gdzie Cov (A, B) - to kowariancja portfeli A i B
- Odchylenie standardowe - to kolejna miara oznaczająca odchylenie od jego średniej. Odchylenie standardowe jest obliczane na podstawie pierwiastka kwadratowego wariancji i oznaczane przez σ.
Kalkulator formuły oczekiwanego zwrotu
Możesz użyć następującego kalkulatora oczekiwanego zwrotu.
| R 1 | |
| P 1 | |
| R 2 | |
| P 2 | |
| R 3 | |
| P 3 | |
| R 4 | |
| P 4 | |
| Spodziewany powrót | |
| Oczekiwany zwrot = | R 1 * P 1 + R 2 * P 2 + R 3 * P 3 + R 4 * P 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Wniosek
Oczekiwany zwrot można zdefiniować jako prawdopodobny zwrot dla portfela posiadanego przez inwestorów na podstawie wcześniejszych zwrotów. Ponieważ wykorzystuje on tylko poprzednie zwroty, dlatego jest to ograniczenie, a wartość oczekiwanego zwrotu nie powinna być jedynym czynnikiem branym pod uwagę przez inwestorów przy podejmowaniu decyzji, czy zainwestować w portfel, czy nie. Należy rozważyć inne miary, takie jak wariancja portfela i odchylenie standardowe.
Polecane artykuły
To był przewodnik po formule Oczekiwany zwrot. Tutaj omawiamy sposób obliczania oczekiwanego zwrotu wraz z praktycznymi przykładami. Oferujemy również kalkulator oczekiwanego zwrotu z szablonem Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przewodnik po formule wskaźnika obrotu aktywami
- Przewodnik po formule Bid Ask Spread
- Jak obliczyć wskaźnik wykorzystania pojemności?
- Obliczanie rentowności obligacji
- Wzór wskaźnika obrotu | Przykłady | Szablon Excel