
Wprowadzenie do funkcji matematycznych w Javie
Java jest jednym z najbardziej przydatnych języków programowania. Ma wiele aplikacji, takich jak budowanie architektury, rozwiązywanie obliczeń w nauce, tworzenie map itp. Aby ułatwić wykonywanie tych zadań, Java udostępnia klasę java.lang.Math lub funkcje matematyczne w Javie, które wykonują kilka operacji, takich jak kwadrat, wykładniczy, sufit, logarytm, sześcian, abs, trygonometria, pierwiastek kwadratowy, podłoga itp. Ta klasa udostępnia dwa pola, które są podstawami klasy matematycznej. Oni są,
- „e”, które jest podstawą logarytmu naturalnego (718281828459045)
- „pi”, które jest stosunkiem obwodu koła do jego średnicy (141592653589793)
Różne funkcje matematyczne w Javie
Java oferuje mnóstwo metod matematycznych. Można je sklasyfikować jak pokazano poniżej:
- Podstawowe metody matematyczne
- Trygonometryczne metody matematyczne
- Logarytmiczne metody matematyczne
- Hiperboliczne metody matematyczne
- Metody matematyki kątowej
Teraz przyjrzyjmy się im szczegółowo.
1. Podstawowe metody matematyczne
Aby lepiej zrozumieć, możemy zaimplementować powyższe metody w programie Java, jak pokazano poniżej:
| metoda | Zwracana wartość | Argumenty |
Przykład |
|
abs () | Wartość bezwzględna argumentu. tj. wartość dodatnia | long, int, float, double |
int n1 = Math.abs (80) // n1 = 80 int n2 = Math.abs (-60) // n2 = 60 |
|
sqrt () | Pierwiastek kwadratowy argumentu | podwójnie |
double n = Math.sqrt (36.0) // n = 6.0 |
|
cbrt () | Korzeń sześcianu argumentu | podwójnie |
double n = Math.cbrt (8.0) // n = 2.0 |
|
max () | Maksymalnie dwie wartości przekazane w argumencie | long, int, float, double |
int n = Math.max (15, 80) // n = 80 |
|
min () | Co najmniej dwie wartości przekazane w argumencie | long, int, float, double |
int n = Math.min (15, 80) // n = 15 |
|
stropować() | Zaokrągla liczbę zmiennoprzecinkową do wartości całkowitej | podwójnie | double n = Math.ceil (6.34) //n=7.0 |
| piętro() | Zaokrągla liczbę zmiennoprzecinkową w dół do wartości całkowitej | podwójnie |
double n = Math.floor (6.34) //n=6.0 |
|
okrągły() | Zaokrągla liczbę zmiennoprzecinkową lub podwójną do wartości całkowitej w górę lub w dół | podwójny, pływakowy | double n = Math.round (22.445); // n = 22.0 double n2 = Math.round (22.545); //n=23.0 |
|
pow () |
Wartość pierwszego parametru podniesiona do drugiego parametru |
podwójnie | double n = Math.pow (2.0, 3.0) //n=8.0 |
|
losowy() | Losowa liczba od 0 do 1 | podwójnie | double n = Math.random () // n = 0.2594036953954201 |
|
signum () | Znak przekazanego parametru.
Jeśli dodatni, wyświetli się 1. Jeśli ujemne, wyświetli się -1. Jeśli 0, wyświetli się 0 | podwójny, pływakowy |
podwójne n = matematyka. signum (22.4); // n = 1, 0 double n2 = Math. signum (-22, 5); // n = -1, 0 |
|
addExact () | Suma parametrów. Wyjątek jest generowany, jeśli uzyskany wynik przepełnia wartość długą lub całkowitą. | int, długo |
int n = Math.addExact (35, 21) // n = 56 |
|
incrementExact () | Parametr zwiększany o 1. Wyjątek jest zgłaszany, jeśli uzyskany wynik przekracza wartość int. | int, długo |
int n = matematyka. incrementExact (36) // n = 37 |
|
subtractExact () | Różnica parametrów. Wyjątek jest zgłaszany, jeśli uzyskany wynik przekracza wartość int. | int, długo |
int n = Math.subtractExact (36, 11) // n = 25 |
|
multiplyExact () | Suma parametrów. Wyjątek jest generowany, jeśli uzyskany wynik przepełnia wartość długą lub całkowitą. | int, długo |
int n = Math.multiplyExact (5, 5) // n = 25 |
|
decrementExact () | Parametr zmniejszony o 1. Wyjątek jest zgłaszany, jeśli uzyskany wynik przekracza wartość int lub long. | int, długo |
int n = matematyka. decrementExact (36) // n = 35 |
|
negateExact () | Negacja parametru. Wyjątek jest zgłaszany, jeśli uzyskany wynik przekracza wartość int lub long. | int, długo |
int n = matematyka. negateExact (36) // n = -36 |
|
copySign () | Wartość bezwzględna pierwszego parametru wraz ze znakiem określonym w drugim parametrze | podwójny, pływakowy |
double d = Math.copySign (29, 3; -17, 0) //n=-29, 3 |
|
floorDiv () | Podziel pierwszy parametr przez drugi parametr i zostanie wykonana operacja podłogi. | long, int |
int n = Math.floorDiv (25, 3) // n = 8 |
|
hypot () | suma kwadratów parametrów i wykonaj operację pierwiastka kwadratowego. Nie powinno tam być pośredniego przelewu lub niedopełnienia. | podwójnie |
double n = Math.hypot (4, 3) //n=5.0 |
|
getExponent () | obiektywny wykładnik. Ten wykładnik jest reprezentowany podwójnie lub zmiennoprzecinkowo | int |
double n = Math.getExponent (50.45) // n = 5 |
Kod:
//Java program to implement basic math functions
public class JavaMathFunctions (
public static void main(String() args) (
int n1 = Math.abs(80);
System.out.println("absolute value of 80 is: "+n1);
int n2 = Math.abs(-60);
System.out.println("absolute value of -60 is: "+n2);
double n3 = Math.sqrt(36.0);
System.out.println("Square root of 36.0 is: "+n3);
double n4 = Math.cbrt(8.0);
System.out.println("cube root 0f 8.0 is: "+n4);
int n5= Math.max(15, 80);
System.out.println("max value is: "+n5);
int n6 =Math.min(15, 80);
System.out.println("min value is: "+n6);
double n7 = Math.ceil(6.34);
System.out.println("ceil value of 6.34 is "+n7);
double n8 = Math.floor(6.34);
System.out.println("floor value of 6.34 is: "+n8);
double n9 = Math.round(22.445);
System.out.println("round value of 22.445 is: "+n9);
double n10 = Math.round(22.545);
System.out.println("round value of 22.545 is: "+n10);
double n11= Math.pow(2.0, 3.0);
System.out.println("power value is: "+n11);
double n12= Math.random();
System.out.println("random value is: "+n12);
double n13 = Math. signum (22.4);
System.out.println("signum value of 22.4 is: "+n13);
double n14 = Math. signum (-22.5);
System.out.println("signum value of 22.5 is: "+n14);
int n15= Math.addExact(35, 21);
System.out.println("added value is: "+n15);
int n16=Math. incrementExact(36);
System.out.println("increment of 36 is: "+n16);
int n17 = Math.subtractExact(36, 11);
System.out.println("difference is: "+n17);
int n18 = Math.multiplyExact(5, 5);
System.out.println("product is: "+n18);
int n19 =Math. decrementExact (36);
System.out.println("decrement of 36 is: "+n19);
int n20 =Math. negateExact(36);
System.out.println("negation value of 36 is: "+n20);
)
)
Wynik:
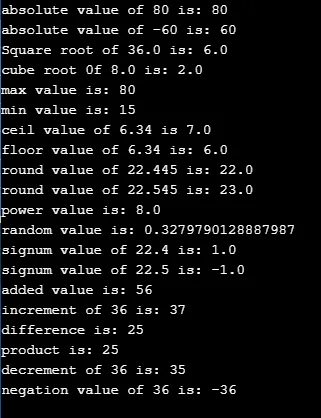
2. Trygonometryczne metody matematyczne
Poniżej przedstawiono program Java do implementacji trygonometrycznych funkcji matematycznych wymienionych w tabeli:
|
metoda | Zwracana wartość | Argumenty | Przykład |
|
grzech() | Wartość sinusoidalna parametru | podwójnie |
podwójna liczba 1 = 60; // Konwersja wartości na radiany podwójna wartość = Math.toRadians (num1); print Math.sine (wartość) // wyjście to 0, 8660254037844386 |
|
sałata() | Wartość cosinus parametru | podwójnie |
podwójna liczba 1 = 60; // Konwersja wartości na radiany podwójna wartość = Math.toRadians (num1); print Math.cos (wartość) // wyjście to 0, 5000000000000001 |
|
dębnik() | wartość styczna parametru | podwójnie |
podwójna liczba 1 = 60; // Konwersja wartości na radiany podwójna wartość = Math.toRadians (num1); print Math.tan (wartość) // wyjście to 1.7320508075688767 |
|
jak w() | Wartość Arc Sinus parametru. Lub Odwrotna wartość sinusoidalna parametru | podwójnie |
Math.asin (1.0) // 1.5707963267948966 |
|
acos () | Wartość cosinus łuku parametru lub wartość cosinus odwrotny parametru | podwójnie |
Math.acos (1.0) //0.0 |
|
atan () | Wartość arcus tangens parametru lub Odwrotna wartość styczna parametru | podwójnie |
Math.atan (6.267) // 1.4125642791467878 |
Kod:
//Java program to implement trigonometric math functions
public class JavaMathFunctions (
public static void main(String() args) (
double num1 = 60;
// Conversion of value to radians
double value = Math.toRadians(num1);
System.out.println("sine value is : "+Math.sin(value));
System.out.println("cosine value is : "+Math.cos(value));
System.out.println("tangent value is : "+Math.tan(value));
double num2 = 1.0;
System.out.println("acosine value is : "+Math.acos(num2));
System.out.println("asine value is : "+Math.asin(num2));
double num3 = 6.267;
System.out.println("atangent value is : "+Math.atan(num3));
Wynik:
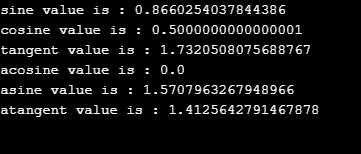
3. Logarytmiczne metody matematyczne
Oto przykładowy program, który implementuje logarytmiczne metody matematyczne:
|
metoda | Zwracana wartość | Argumenty |
Przykład |
|
expm1 () | Oblicz moc E. i odejmij 1 od niej. E jest liczbą Eulera. Więc tutaj jest e x -1. | podwójnie |
double n = Math.expm1 (2.0) // n = 6.38905609893065 |
|
exp () | Moc E do danego parametru. To znaczy, ex | podwójnie |
double n = Math.exp (2.0) // n = 7.38905609893065 |
|
log() | Logarytm naturalny parametru | podwójnie |
double n = Math.log (38, 9) //n=3.6609942506244004 |
|
log10 () | Podstawa 10 logarytmu parametru | podwójnie |
double n = Math.log10 (38, 9) // n = 1, 5899496013257077 |
|
log1p () | Logarytm naturalny sumy parametru i jednego. ln (x + 1) | podwójnie |
double n = Math.log1p (26) // n = 3.295836866004329 |
Kod://Java program to implement logarithmic math functions
public class JavaMathFunctions (
public static void main(String() args) (
double n1 = Math.expm1(2.0);
double n2 = Math.exp(2.0);
double n3 = Math.log(38.9);
double n4 = Math.log10(38.9);
double n5 = Math.log1p(26);
System.out.println("expm1 value of 2.0 is : "+n1);
System.out.println("exp value of 2.0 is : "+n2);
System.out.println("log of 38.9 is : "+n3);
System.out.println("log10 of 38.9 is : "+n4);
System.out.println("log1p of 26 is : "+n5);
))
Wynik:
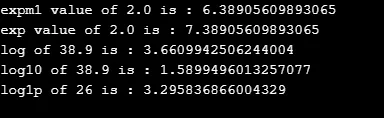
4. Hiperboliczne metody matematyczne
Poniżej przedstawiono program Java do implementacji hiperbolicznych funkcji matematycznych wymienionych w tabeli:
|
metoda | Zwracana wartość | Argumenty |
Przykład |
|
sinh () | Wartość sinus hiperboliczny parametru. tj. (ex - e -x) / 2 Tutaj E jest liczbą Eulera. | podwójnie |
double num1 = Math.sinh (30) // wyjście to 5.343237290762231E12 |
|
pałka() | Hiperboliczna wartość kosinusowa parametru. tj. (ex + e -x) / 2 Tutaj E jest liczbą Eulera. | podwójnie |
double num1 = Math.cosh (60.0) // wyjście to 5.710036949078421E25 |
|
tanh () | Hiperboliczna wartość styczna parametru | podwójnie |
double num1 = Math.tanh (60.0) // wyjście to 1.0 |
Kod:
//Java program to implement HYPERBOLIC math functions
public class JavaMathFunctions (
public static void main(String() args) (
double n1 = Math.sinh (30);
double n2 = Math.cosh (60.0);
double n3 = Math.tanh (60.0);
System.out.println("Hyperbolic sine value of 300 is : "+n1);
System.out.println("Hyperbolic cosine value of 60.0 is : "+n2);
System.out.println("Hyperbolic tangent value of 60.0 is : "+n3);
)
)
Wynik:

5. Metody matematyki kątowej
| metoda | Zwracana wartość | Argumenty | Przykład |
| toRadians () | Kąt stopnia przekształca się w kąt radianowy | podwójnie |
double n = Math.toRadians (180.0) // n = 3.141592653589793 |
| toDegrees () | Kąt radianowy jest konwertowany na kąt stopniowy | podwójnie |
podwójne n = matematyka. toDegrees (Math.PI) //n=180.0 |
Zobaczmy teraz przykładowy program demonstrujący metody matematyki kątowej.
Kod:
//Java program to implement Angular math functions
public class JavaMathFunctions (
public static void main(String() args) (
double n1 = Math.toRadians(180.0);
double n2 = Math. toDegrees (Math.PI);
System.out.println("Radian value of 180.0 is : "+n1);
System.out.println("Degree value of pi is : "+n2);
)
)
Wynik:

Wniosek
Java oferuje szeroką gamę funkcji matematycznych do wykonywania różnych zadań, takich jak obliczenia naukowe, projektowanie architektury, projektowanie konstrukcji, mapy budynków itp. W tym dokumencie omawiamy szczegółowo kilka podstawowych, trygonometrycznych, logarytmicznych i kątowych funkcji matematycznych z przykładowymi programami i przykłady.
Polecane artykuły
Jest to przewodnik po funkcjach matematycznych w Javie. Tutaj omawiamy 5 metod działania matematyki w Javie z kodami i wyjściami. Możesz również przejrzeć nasze inne powiązane artykuły, aby dowiedzieć się więcej-
- Anonimowe funkcje w Matlabie
- Funkcje tablic w C
- Funkcje matematyczne PHP
- Różne funkcje matematyczne w języku Python
- Przegląd funkcji matematycznych w C
- Wprowadzenie do funkcji matematycznych w języku C #
- Pierwiastek kwadratowy w PHP