Regresja liniowa w programie Excel - Jak wykonać regresję liniową w programie Excel?

Regresja liniowa w programie Excel (spis treści)

Wprowadzenie do regresji liniowej w programie Excel
Metody użycia regresji liniowej w programie Excel

Wprowadzenie do regresji liniowej w programie Excel

Regresja liniowa jest techniką / metodą statystyczną stosowaną do badania związku między dwiema ciągłymi zmiennymi ilościowymi. W tej technice zmienne niezależne są używane do przewidywania wartości zmiennej zależnej. Jeśli istnieje tylko jedna zmienna niezależna, jest to prosta regresja liniowa, a jeśli wiele zmiennych niezależnych jest więcej niż jedna, to jest to wielokrotna regresja liniowa. Modele regresji liniowej mają związek między zmiennymi zależnymi i niezależnymi poprzez dopasowanie równania liniowego do obserwowanych danych. Liniowy oznacza fakt, że używamy linii, aby dopasować nasze dane. Zmienne zależne stosowane w analizie regresji nazywane są również zmiennymi odpowiedzi lub przewidywanymi, a zmienne niezależne nazywane są również zmiennymi objaśniającymi lub predyktorami.

Linia regresji liniowej ma równanie rodzaju: Y = a + bX;

Gdzie:

X jest zmienną objaśniającą,
Y jest zmienną zależną,
b to nachylenie linii,
a jest przecięciem y (tj. wartością y, gdy x = 0).

Metodę najmniejszych kwadratów stosuje się zwykle w regresji liniowej, która oblicza linię najlepszego dopasowania dla obserwowanych danych, minimalizując sumę kwadratów odchylenia punktów danych od linii.

Metody użycia regresji liniowej w programie Excel

W tym przykładzie przedstawiono metody przeprowadzania analizy regresji liniowej w programie Excel. Spójrzmy na kilka metod.

Możesz pobrać ten szablon Excel z regresją liniową tutaj - Szablon Excel z regresją liniową

Metoda nr 1 - Wykres rozproszenia z linią trendu

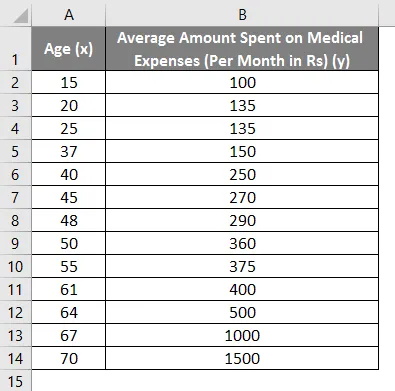
Powiedzmy, że mamy zestaw danych niektórych osób z ich wiekiem, wskaźnikiem biomasy (BMI) i kwotą wydaną przez nich na wydatki medyczne w ciągu miesiąca. Teraz dzięki wglądowi w cechy osób, takie jak wiek i BMI, chcemy dowiedzieć się, w jaki sposób te zmienne wpływają na wydatki medyczne, a tym samym wykorzystać je do przeprowadzenia regresji i oszacowania / przewidzenia średnich wydatków medycznych dla niektórych konkretnych osób. Zobaczmy najpierw, jak tylko wiek wpływa na wydatki medyczne. Zobaczmy zestaw danych:

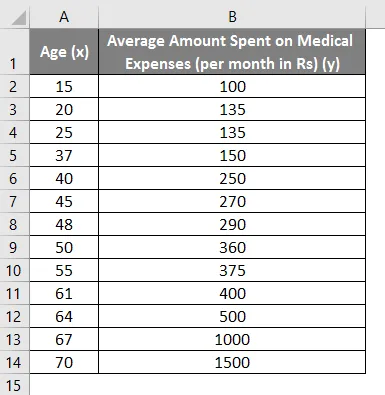
Kwota na wydatki medyczne = b * wiek + a

Wybierz dwie kolumny zestawu danych (xiy), w tym nagłówki.

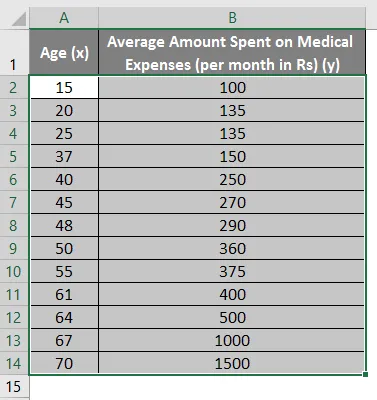
Kliknij „Wstaw” i rozwiń menu „Scatter Chart” i wybierz miniaturę „Scatter” (pierwsza)

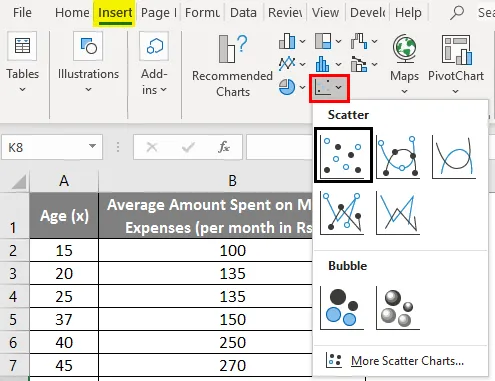
Teraz pojawi się wykres rozproszenia i narysujemy na tym linię regresji. Aby to zrobić, kliknij prawym przyciskiem myszy dowolny punkt danych i wybierz „Dodaj linię trendu”

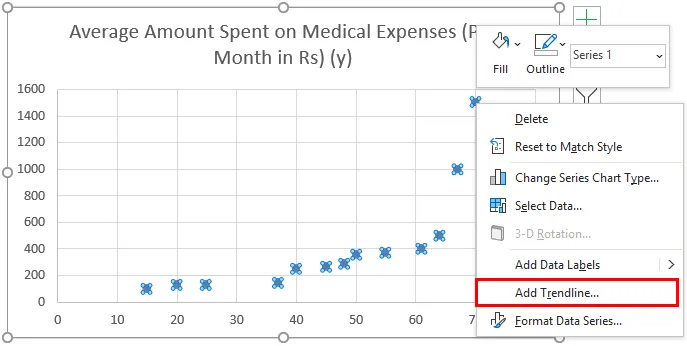
Teraz w panelu „Formatuj linię trendu” po prawej stronie wybierz „Liniowa linia trendu” i „Wyświetl równanie na wykresie”.

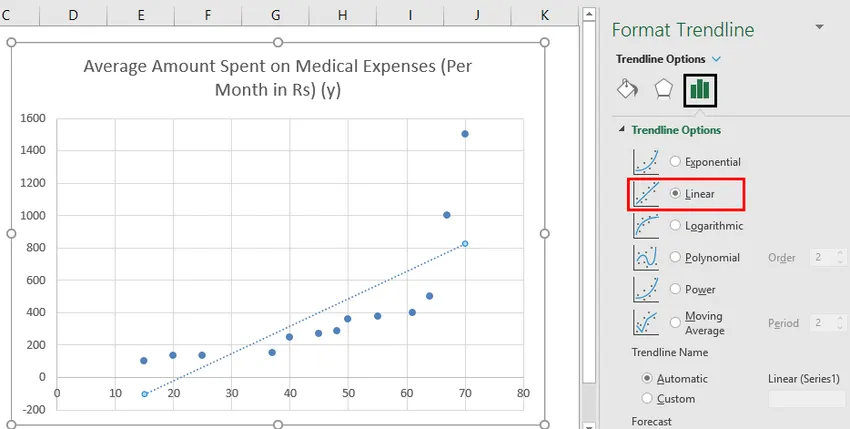
Wybierz „Wyświetl równanie na wykresie”.

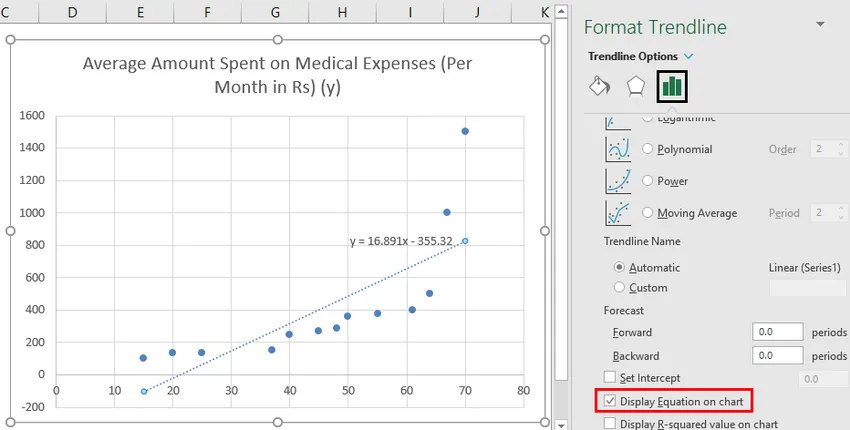
Możemy improwizować tabelę zgodnie z naszymi wymaganiami, na przykład dodając tytuły osi, zmieniając skalę, kolor i rodzaj linii.

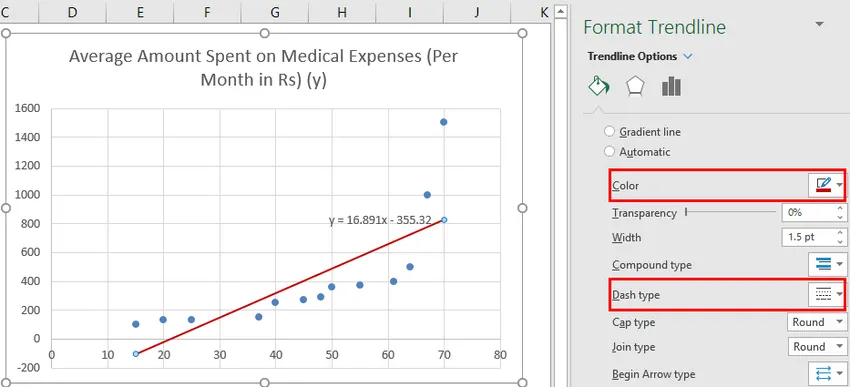
Po ulepszeniu wykresu otrzymujemy wynik.

Uwaga: W tego typu wykresie regresji zmienna zależna powinna zawsze znajdować się na osi y i niezależna od osi x. Jeśli wykres zostanie wykreślony w odwrotnej kolejności, albo przełącz osie na wykresie, albo zamień kolumny w zestawie danych.

Metoda nr 2 - Metoda analizy dodatku ToolPak

Analysis ToolPak czasami nie jest domyślnie włączony i musimy to zrobić ręcznie. Aby to zrobić:

Kliknij menu „Plik”.

Następnie kliknij „Opcje”.

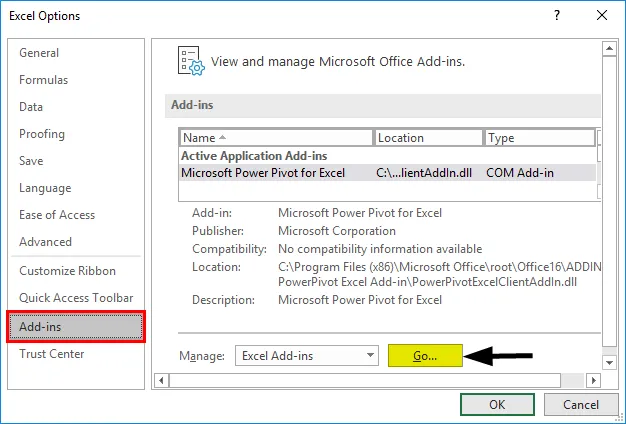
Wybierz „Dodatki Excela” w polu „Zarządzaj” i kliknij „Idź”

Wybierz „Analysis ToolPak” -> „OK”

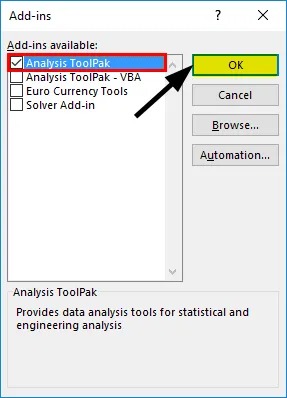
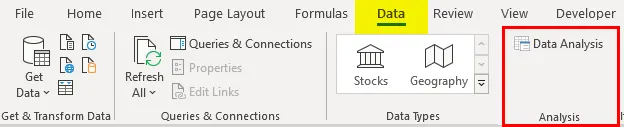
Spowoduje to dodanie narzędzi „Analiza danych” do karty „Dane”. Teraz przeprowadzamy analizę regresji:

Kliknij „Analiza danych” w zakładce „Dane”

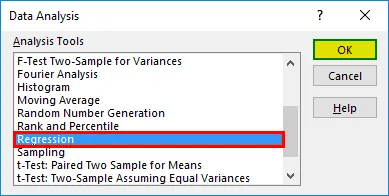
Wybierz „Regresja” -> „OK”

Pojawi się okno dialogowe regresji. Wybierz zakres wejściowy Y i zakres wejściowy X (odpowiednio koszty leczenia i wiek). W przypadku wielokrotnej regresji liniowej możemy wybrać więcej kolumn zmiennych niezależnych (np. Jeśli chcemy zobaczyć wpływ BMI również na wydatki medyczne).
Zaznacz pole „Etykiety”, aby dołączyć nagłówki.
Wybierz żądaną opcję „wyjścia”.
Zaznacz pole wyboru „pozostałości” i kliknij „OK”.

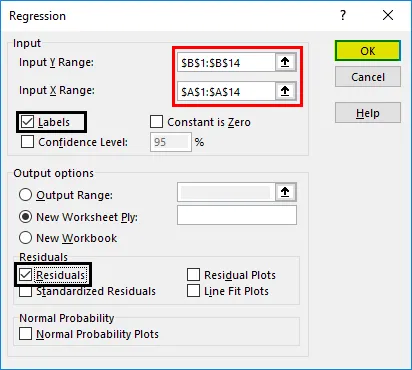
Teraz nasze wyniki analizy regresji zostaną utworzone w nowym arkuszu, zawierającym statystyki regresji, ANOVA, wartości rezydualne i współczynniki.

Interpretacja wyjściowa:

Statystyki regresji pokazują, jak dobrze równanie regresji pasuje do danych:

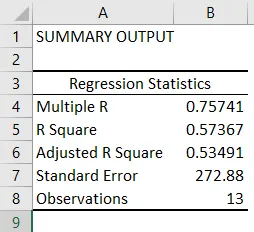
Wielokrotność R jest współczynnikiem korelacji mierzącym siłę zależności liniowej między dwiema zmiennymi. Leży między -1 a 1, a jego wartość bezwzględna przedstawia siłę związku z dużą wartością wskazującą na silniejszy związek, niską wartością wskazującą ujemną i zerową wartością wskazującą brak związku.
R Kwadrat to współczynnik determinacji stosowany jako wskaźnik dobroci dopasowania. Leży między 0 a 1, a wartość zbliżona do 1 wskazuje, że model jest dobrze dopasowany. W tym przypadku 0, 57 = 57% wartości y wyjaśniono wartościami x.
Skorygowany kwadrat R to skorygowany kwadrat R dla liczby predyktorów w przypadku wielokrotnej regresji liniowej.
Błąd standardowy przedstawia dokładność analizy regresji.
Obserwacje obrazują liczbę obserwacji modelowych.
Anova określa poziom zmienności w modelu regresji.

Z reguły nie stosuje się tego do prostej regresji liniowej. Jednak „Istotne wartości F” wskazują, jak wiarygodne są nasze wyniki, a wartość większa niż 0, 05 sugeruje wybranie innego predyktora.

Współczynniki są najważniejszą częścią używaną do budowy równania regresji.

Zatem nasze równanie regresji byłoby następujące: y = 16, 891 x - 355, 32. Jest to to samo, co w metodzie 1 (wykres rozproszenia z linią trendu).

Teraz, jeśli chcemy przewidzieć średnie wydatki medyczne w wieku 72 lat:

Zatem y = 16, 891 * 72 -355, 32 = 860, 832

W ten sposób możemy przewidzieć wartości y dla dowolnych innych wartości x.

Resztki wskazują różnicę między wartościami rzeczywistymi i przewidywanymi.

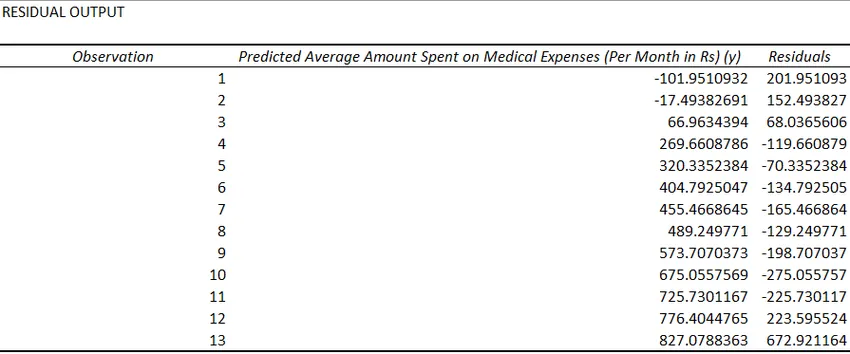
Ostatnia metoda regresji nie jest tak często stosowana i wymaga funkcji statystycznych, takich jak slope (), intercept (), correl () itp., Aby przeprowadzić analizę regresji.

O czym należy pamiętać o regresji liniowej w programie Excel

Analiza regresji jest zwykle stosowana do sprawdzenia, czy istnieje statystycznie istotny związek między dwoma zestawami zmiennych.
Służy do przewidywania wartości zmiennej zależnej na podstawie wartości jednej lub więcej zmiennych niezależnych.
Ilekroć chcemy dopasować model regresji liniowej do grupy danych, należy dokładnie obserwować zakres danych, tak jakbyśmy używali równania regresji do przewidywania dowolnej wartości poza tym zakresem (ekstrapolacja), może to prowadzić do błędnych wyników.

Polecane artykuły

Jest to przewodnik po regresji liniowej w programie Excel. Tutaj omawiamy sposób regresji liniowej w programie Excel wraz z praktycznymi przykładami i szablonem Excela do pobrania. Możesz także przejrzeć nasze inne sugerowane artykuły -