
Przykładowa formuła odchylenia standardowego (spis treści)
- Formuła
- Przykłady
Przykładowa formuła odchylenia standardowego
W statystyce odchylenie standardowe jest w zasadzie miarą znalezienia dyspersji wartości zestawu danych od średniej wartości zestawu danych. Mierzy odległość tego punktu danych i średnią. Im wyższe odchylenie standardowe, tym większa będzie dyspersja, a punkty danych będą miały tendencję do dalekiej od średniej. Podobnie niższe odchylenie standardowe oznacza, że punkty danych będą bliższe średniej. Jest to bardzo przydatne w porównaniu zestawów danych, które mogą mieć tę samą wartość średnią, ale inny zakres.
Zwykle oblicz standardowe odchylenie danych populacji, ale czasami dane populacji są tak ogromne, że nie można znaleźć dla tego standardowego odchylenia. W takim przypadku obliczane jest odchylenie standardowe próbki, które stanie się reprezentatywne dla odchylenia standardowego populacji. Zakładamy, że próbka jest prawidłową reprezentacją populacji i skupimy się na odchyleniu standardowym próbki w tym artykule.
Załóżmy, że masz zestaw danych X z punktami danych (X1, X2 …… ..Xn).
Wzór na odchylenie standardowe populacji podaje:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Jeśli nie otrzymałeś całej populacji i masz tylko próbkę (powiedzmy, że X to przykładowy zestaw danych populacji), to wzór na odchylenie standardowe próbki podaje:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Gdzie:
- X i - i- ta wartość zestawu danych
- X m - średnia wartość zestawu danych
- n - Całkowita liczba punktów danych
Formuła może początkowo wydawać się myląca, ale naprawdę należy nad nią popracować. Poniżej przedstawiono kroki, które można wykonać, aby obliczyć odchylenie standardowe próbki:
- Znajdź liczbę punktów w zbiorze danych, tj. N
- Następnie następnym krokiem jest znalezienie średniej wartości próbki. Jest to w zasadzie średnia wszystkich wartości.
- Następnie dla każdego punktu danych znajdź różnicę od średniej, a następnie wyrównaj.
- Zsumuj wszystkie wartości w powyższym kroku i podziel to przez n-1.
- Ostatnim krokiem jest obliczenie pierwiastka kwadratowego z liczby obliczonej powyżej.
Istnieje inny sposób obliczenia populacji i odchylenia standardowego, po prostu za pomocą funkcji STDEV.P () dla odchylenia standardowego populacji i funkcji STDEV.S () dla odchylenia standardowego próbki w programie Excel.
Przykłady przykładowej formuły odchylenia standardowego (z szablonem Excel)
Weźmy przykład, aby lepiej zrozumieć obliczenie odchylenia standardowego próbki.
Możesz pobrać ten przykładowy szablon Excel z formułą odchylenia standardowego - przykładowy szablon Excel z formułą odchylenia standardowegoPrzykładowa formuła odchylenia standardowego - przykład nr 1
Załóżmy, że mamy dwa przykładowe zestawy danych A i B, a każdy z nich zawiera 20 losowych punktów danych i ma tę samą średnią. Oblicz przykładowe odchylenie standardowe dla zestawu danych A i B.
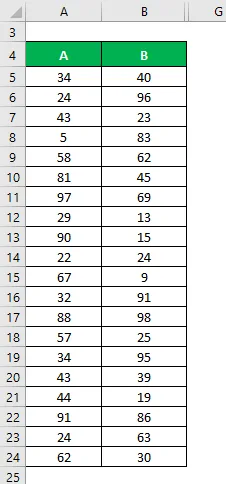
Rozwiązanie:
Średnia jest obliczana jako:
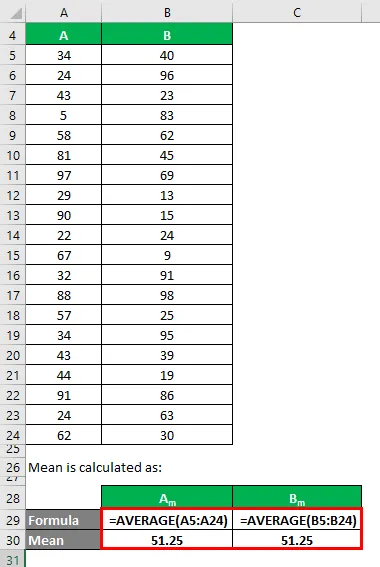
- Średnia zestawu danych A = 51, 25
- Średnia zestawu danych B = 51, 25
Teraz musimy obliczyć różnicę między punktami danych a wartością średnią.
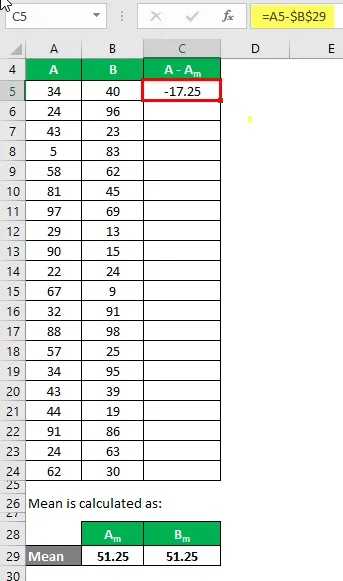
Podobnie obliczyć dla wszystkich zestawów danych A.
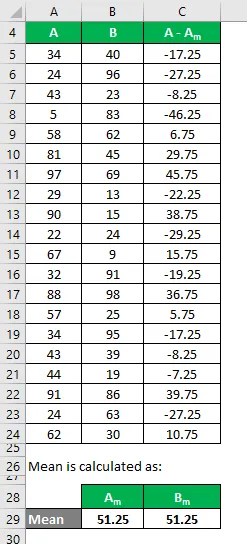
Podobnie obliczyć go również dla zestawu danych B.
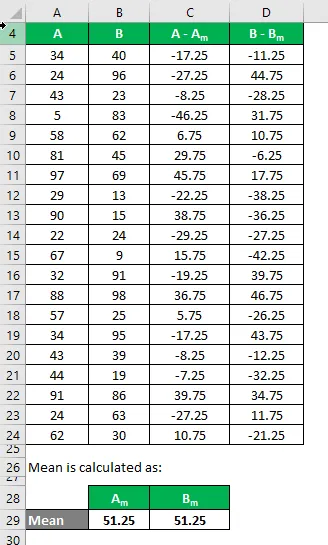
Oblicz kwadrat różnicy dla obu zestawów danych A i B.
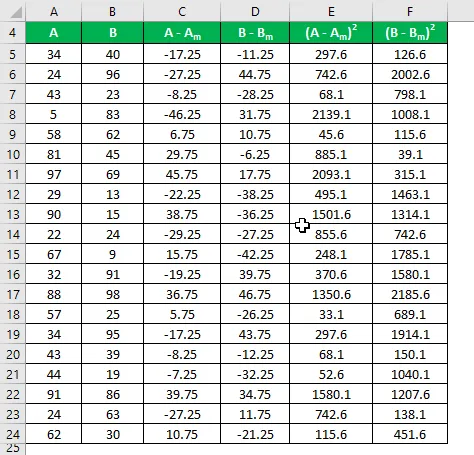
Odchylenie standardowe próbki oblicza się przy użyciu poniższego wzoru
Przykładowe odchylenie standardowe = √ (Σ (X i - X m ) 2 / (n - 1))
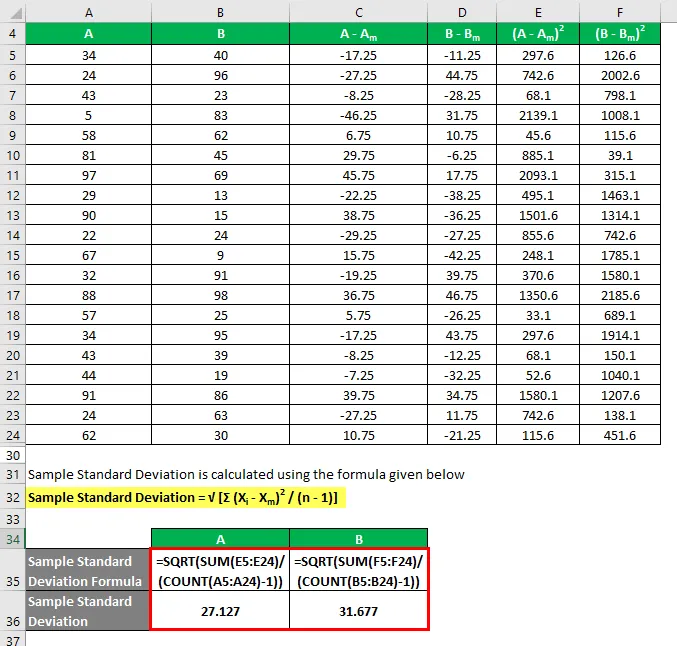
Więc jeśli tu zobaczysz, chociaż oba zestawy danych mają tę samą wartość średnią, B ma bardziej standardowe odchylenie niż A, co oznacza, że punkty danych B są bardziej rozproszone niż A.
Przykładowa formuła odchylenia standardowego - przykład nr 2
Powiedzmy, że jesteś bardzo niechętnym do inwestowania inwestorem i chcesz zainwestować pieniądze na giełdzie. Ponieważ twój apetyt na ryzyko jest niski, chcesz inwestować w bezpieczne akcje o niższym standardowym odchyleniu. Twój doradca finansowy zaproponował ci 4 akcje, z których możesz wybierać. Chcesz wybrać 2 akcje spośród 4 i zdecydujesz, że na podstawie niższego odchylenia standardowego.
Masz informacje na temat ich historycznych zysków z ostatnich 15 lat.
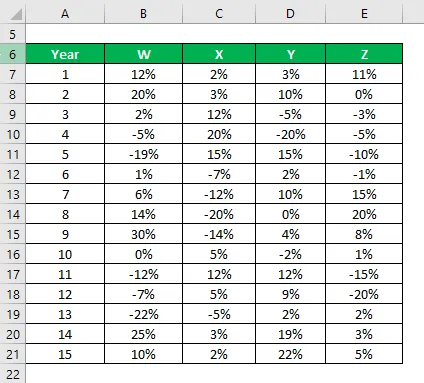
Rozwiązanie:
Odchylenie standardowe próbki oblicza się przy użyciu wzoru Excela
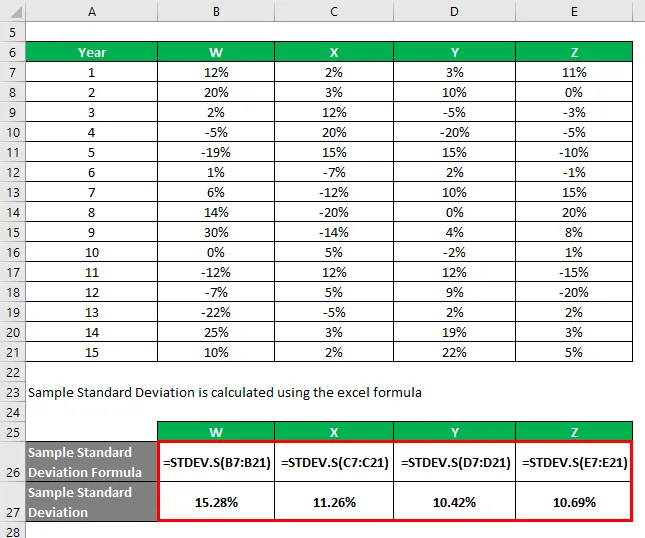
Na podstawie informacji i przykładowego odchylenia standardowego wybierzesz akcje Y i Z do zainwestowania, ponieważ mają one najniższe odchylenie standardowe.
Wyjaśnienie
Omawiamy znaczenie odchylenia standardowego z statystycznego punktu widzenia, ale odgrywa on również istotną rolę, jeśli mówimy o finansowym punkcie widzenia. W finansach jest to w zasadzie miara ryzyka, jakie niesie inwestycja, oraz stopień jej ryzyka. Na podstawie ryzyka inwestycji inwestorzy mogą następnie obliczyć minimalny zwrot wymagany do zrekompensowania tego ryzyka. Jak w powyższym przykładzie, ponieważ Y i Z mają mniejsze odchylenie standardowe, oznacza to, że zwroty tych zapasów są mniej zmienne, więc są mniej ryzykowne. Podczas korzystania ze standardowego narzędzia do odchylania należy pamiętać, że na ekstremalne wartości lub wartości odstające mają duży wpływ. Te wartości odstające mogą wypaczać wartość odchylenia standardowego.
Trafność i zastosowania wzoru odchylenia standardowego próbki
Odchylenie standardowe pomaga inwestorom i analitykowi znaleźć współczynnik ryzyka i zysku lub współczynnik Sharpe dla inwestycji. Zasadniczo każdy może zarobić na stopie zwrotu wolnej od ryzyka, inwestując w Skarb Państwa i papiery wartościowe wolne od ryzyka. Ale zwrot ponad to zwrot nadwyżki i aby to osiągnąć, jaki poziom ryzyka należy podjąć, jest miarą współczynnika Sharpe'a:
Wskaźnik Sharpe'a = (zwrot z inwestycji - stopa wolna od ryzyka) / odchylenie standardowe
Im wyższy wskaźnik Sharpe'a, tym lepsza jest inwestycja.
Jak powiedzieliśmy, odchylenie standardowe jest miarą ryzyka, ale niższa wartość odchylenia standardowego nie zawsze jest preferowana. Jeśli inwestor ma większy apetyt na ryzyko i chce inwestować bardziej agresywnie, będzie skłonny podjąć większe ryzyko i preferuje stosunkowo wyższe odchylenie standardowe niż inwestor unikający ryzyka. Wszystko zależy więc od poziomu ryzyka, jaki inwestor jest skłonny podjąć.
Polecane artykuły
Jest to przewodnik po próbce wzoru odchylenia standardowego. Tutaj omawiamy sposób obliczania przykładowego odchylenia standardowego wraz z praktycznymi przykładami i szablonem programu Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Przykłady wzoru wariancji populacji
- Kalkulator względnego odchylenia standardowego
- Jak obliczyć standardowy rozkład normalny?
- Obliczanie rozkładu dwumianowego