Formuła CAPM (spis treści)
- Formuła CAPM
- Kalkulator CAPM
- Formuła CAPM w programie Excel (z szablonem Excel)
Formuła CAPM
Liniową zależność między oczekiwanym zwrotem z inwestycji a jego ryzykiem systemowym reprezentuje formuła Modelu wyceny kapitału (CAPM).
CAPM oblicza się zgodnie z poniższym wzorem:
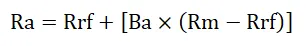
Gdzie:
- Ra = oczekiwany zwrot z inwestycji
- Rrf = stopa wolna od ryzyka
- Ba = Beta inwestycji
- Rm = oczekiwany zwrot z rynku
A premia za ryzyko to różnica między oczekiwanym zwrotem z rynku minus stopa wolna od ryzyka (Rm - Rrf) .
Premia za ryzyko rynkowe
Premia za ryzyko rynkowe to nadwyżka zwrotu, tj. Nagroda, która ma zrekompensować inwestorowi ryzyko związane z portfelem, ponieważ inwestowanie na giełdzie jest zawsze wyższe niż inwestowanie w obligacje rządowe. Dlatego jest to różnica między oczekiwanym zwrotem z rynku a stopą wolną od ryzyka. Rynkową stopę zwrotu Rm można oszacować na podstawie przeszłych zwrotów lub prognozowanych przyszłych zwrotów. Na przykład bony i obligacje skarbowe USA są stosowane do stopy wolnej od ryzyka.
Spodziewany powrót
„Ra” odnosi się do oczekiwanego zwrotu z inwestycji w danym okresie.
Stopa wolna od ryzyka
„Rrf” oznacza stopę wolną od ryzyka, która jest równa rentowności 10-letniego amerykańskiego bonu skarbowego lub obligacji skarbowej. Stopa wolna od ryzyka to zwrot z inwestycji, która nie przynosi żadnego ryzyka, ale w świecie rzeczywistym obejmuje ryzyko inflacji. Stopa wolna od ryzyka powinna być również krajem, w którym dokonywana jest inwestycja, a okres zapadalności obligacji powinien również odpowiadać okresowi inwestycji. Zwykle stopa zwrotu wolna od ryzyka stosowana do oszacowania premii za ryzyko jest zwykle średnią historycznych stóp zwrotu bez ryzyka, a nie ogólnie bieżącą stopą zwrotu wolną od ryzyka.
Beta
Beta, która jest reprezentowana jako „Ba” we wzorach CAPM, jest miarą zmienności papieru wartościowego lub portfela i jest obliczana na podstawie pomiaru zmiany ceny akcji wraz ze zwrotem z całego rynku. Beta jest miarą ryzyka systemowego. Na przykład, jeśli beta firmy jest równe 1, 7, oznacza to, że ma 170% zmienności zwrotów średniej rynkowej, a zmiany cen akcji będą raczej skrajne. Jeśli beta wynosi 1, to oczekiwany zwrot z inwestycji jest równy zwrotowi średniej rynkowej. Jeśli beta wynosi -1, oznacza to, że ceny akcji są mniej ryzykowne i zmienne.
Zastosowanie modelu CAPM
Zobaczymy kilka przykładów CAPM, które są najczęściej wykorzystywane do ustalenia, jaka powinna być uczciwa cena inwestycji. Gdy obliczamy stopę zwrotu ryzykownego składnika aktywów przy użyciu CAPM, można ją również wykorzystać do zdyskontowania przyszłych przepływów pieniężnych inwestycji do ich wartości bieżącej i ostatecznie do ustalenia uczciwej ceny inwestycji.
Przykłady formuły CAPM
Weźmy przykład, aby dowiedzieć się o CAPM dla firmy: -
Możesz pobrać ten szablon Excel Formula CAPM tutaj - Szablon Excel Formula CAPMPrzykład 1
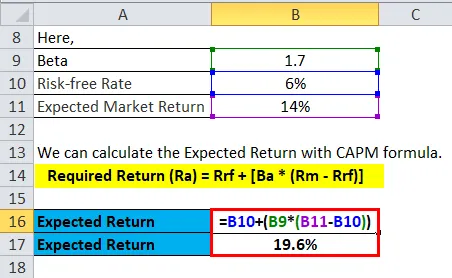
Załóżmy, że oczekuje się, że akcje A przyniosą zwrot w wysokości 14% w przyszłym roku i że obecna stopa wolna od ryzyka wynosi 6%, i chcesz obliczyć, czy opłaca się inwestować w to. Obliczyłeś wartość beta akcji, która wynosi 1, 7. Ogólny rynek akcji ma współczynnik beta 1, 0. Oznacza to, że zapasy wiążą się z wyższym poziomem ryzyka niż ryzyko ogólne. Dlatego oczekujemy wyższego zwrotu niż przewidywany 14% zwrot rynkowy w przyszłym roku.
Oczekiwany zwrot można obliczyć w następujący sposób:
- Wymagany zwrot (Ra) = Rrf + (Ba * (Rm - Rrf))
- Wymagany zwrot (Ra) = 6% + 1, 7 * (14% - 6%)
- Wymagany zwrot (Ra) = 6% + 13, 6%
- Wymagany zwrot (Ra) = 19, 6%
Z tych obliczeń wynika, że uzyskasz 19, 6% na swojej inwestycji. Ca
Przykład 2
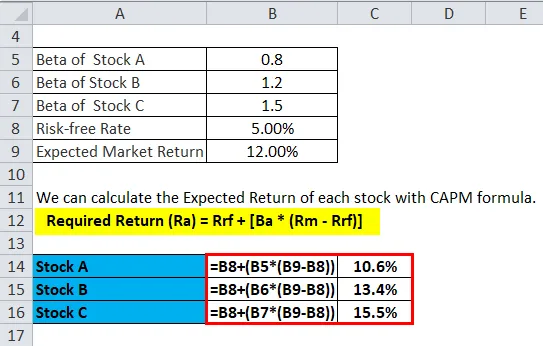
Załóżmy, że inwestor myśli o zainwestowaniu w jedną z trzech akcji dostępnych na rynku. Poniższe informacje są dostępne w celu oszacowania stopy zwrotu z trzech zapasów.
- Zapas A z beta 0, 80
- Zapas B z beta 1, 20
- Zapas C z beta 1, 50
Stopa wolna od ryzyka wynosi 5, 00%, a oczekiwany zwrot z rynku wynosi 12, 00%.
Możemy obliczyć oczekiwany zwrot każdego towaru za pomocą formuły CAPM.
- Wymagany zwrot (Ra) = Rrf + (Ba * (Rm - Rrf))
Oczekiwany zwrot towaru A
- E (RA) = 5, 0% + 0, 80 * (12, 00% - 5, 0%)
- E (RA) = 5, 0% + 5, 6%
- E (RA) = 10, 6%
Oczekiwany zwrot towaru B
- E (R B ) = 5, 0% + 1, 20 * (12, 00% - 5, 0%)
- E (R B ) = 5, 0% + 8, 4%
- E (R B ) = 13, 4%
Oczekiwany zwrot towaru C
- E (R C ) = 5, 0% + 1, 50 * (12, 00% - 5, 0%)
- E (R C ) = 5, 0% + 10, 5%
- E (R C ) = 15, 5%
Dlatego widzimy, że najlepiej inwestować w akcje C. Tak więc widać, że im wyższa beta, tym wyższy oczekiwany zwrot według formuły CAPM.
Przykład 3
Teraz zobaczymy problem z aplikacją oczekiwanego zwrotu. Możemy obliczyć wartość bieżącą netto przy użyciu oczekiwanego zwrotu lub stopy przeszkody ze wzoru CAPM jako stopy zdyskontowanej w celu oszacowania wartości bieżącej netto inwestycji
Podane są następujące informacje:
- β = 1, 3
- Rrf = 6%
- Rm = 13%
Tak więc stawkę przeszkód lub oczekiwany zwrot z projektu oblicza się w następujący sposób:
- Wymagany zwrot (Ra) = Rrf + (Ba * (Rm - Rrf))
- Ra = 6% + 1, 3 * (13% - 6%)
- Ra = 6% + 9, 1%
- Ra = 15, 1%
Informacje dotyczące projektu, który zamierzasz zainwestować, są następujące. Liczby są w lachach:
- Inwestycja początkowa = 5000 funtów
- Oczekiwane płatności dokonane: ₹ 6000 w drugim roku, ₹ 5000 w piątym roku
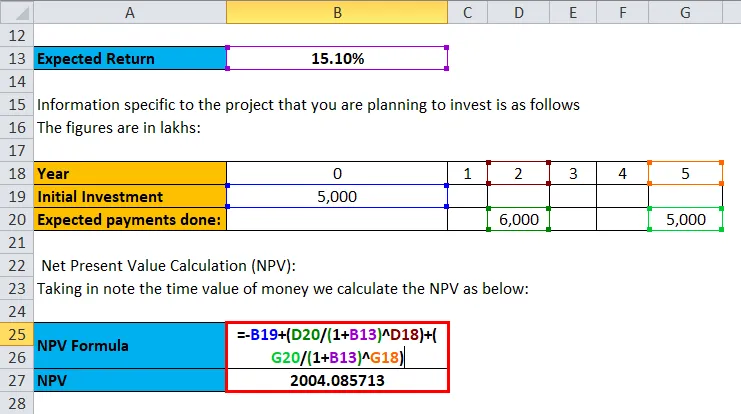
Obliczanie wartości bieżącej netto (NPV): Biorąc pod uwagę wartość pieniądza w czasie, obliczamy NPV w następujący sposób:
Npv = - inwestycja początkowa + suma (wartość inwestycji / (stopa 1+) liczba lat)
Tak więc początkowa inwestycja wynosi 5000, a następnie 6000 jest inwestowane w drugim roku, a 5000 w piątym roku. po prostu wstaw wartości, aby uzyskać wyniki
- NPV = -5, 000 + (6000 / 1, 151 2) + (5000 / 1, 151 5)
- NPV = ₹ 2004.085713
Dlatego wartość netto dokonanych inwestycji wynosi .0 2004.085713.
Założenia formuły CAPM
- Inwestorzy dokonują dywersyfikacji w ramach szeregu inwestycji, aby wyeliminować niesystematyczne ryzyko.
- Inwestorzy mogą pożyczać i pożyczać dowolne kwoty według stopy wolnej od ryzyka.
- CAPM uważa rynek za idealny i nie obejmuje podatków ani kosztów transakcji na rachunku.
- Załóż, że wszystkie informacje są dostępne jednocześnie dla wszystkich inwestorów.
- Każdy inwestor jest przeciwny narażeniu na ryzyko.
Ograniczenia
Ograniczeniem tej formuły CAPM jest wyższe ryzyko związane z aktywami, tym większy oczekiwany zwrot, który nie zawsze jest prawdziwy.
Kalkulator formuł CAPM
Możesz użyć następującego kalkulatora CAPM
| Rrf (%) | |
| Ba | |
| Rm (%) | |
| Ra | |
| Ra = Rrf + (Ba X (Rm - Rrf)) |
| 0 + (0 X (0 - 0)) = 0 |
Formuła CAPM w programie Excel (z szablonem Excel)
Tutaj zrobimy ten sam przykład formuły CAPM w Excelu. To jest bardzo łatwe i proste. Musisz podać trzy dane wejściowe, tj. Stopę wolną od ryzyka, Beta inwestycji i oczekiwany zwrot z rynku
Możesz łatwo obliczyć CAPM za pomocą Formula w podanym szablonie.
Oczekiwany zwrot można obliczyć w następujący sposób:
Możemy obliczyć oczekiwany zwrot każdego towaru za pomocą formuły CAPM.
Oczekiwany zwrot z projektu oblicza się w następujący sposób:

Wartość netto inwestycji oblicza się jako:
Polecane artykuły
To był przewodnik po formule CAPM. Tutaj omawiamy jego zastosowania wraz z praktycznymi przykładami. Oferujemy również kalkulator CAPM z szablonem Excel do pobrania. Możesz także przejrzeć następujące artykuły, aby dowiedzieć się więcej -
- Wzór na wskaźnik zadłużenia
- Przewodnik po formule ekwiwalentu podatkowego
- Przykłady formuły ceny do zysku
- Wzór na średnią aktywów