
Wprowadzenie do funkcji matematycznych w C
W tym artykule wymieniono różne funkcje matematyczne używane w językach programowania C wraz z ilustracją działającego kodu. Komputery wykonują ogromne obliczenia matematyczne i analizy wielkich liczb, aby to zrobić, wykorzystaliśmy funkcje matematyczne w C. Przed rozpoczęciem musimy wiedzieć, że języki C używają nagłówka / biblioteki Math.h do różnych funkcji matematycznych. Pomaga to w obliczaniu operacji trygonometrycznych, logarytmów, wartości bezwzględnych, pierwiastków kwadratowych. Przeanalizujmy różne typy funkcji używanych w tej bibliotece. Wszystkie te funkcje biorą podwójnie jako typ danych i zwracają to samo.
Różne funkcje matematyczne w C
Zobaczmy różne funkcje zdefiniowane w math.h, a biblioteka Math jest podzielona na trzy główne typy: funkcje trygonometryczne, funkcje matematyczne, funkcje Log / expo. Aby wdrożyć poniższe funkcje, konieczne jest włączenie lub umieszczenie w kodzie.
1. piętro (podwójne a)
Ta funkcja zwraca największą wartość całkowitą nie większą niż wartość „a”. Zaokrągla wartość i zwraca wynik podwójny. Zachowuje się inaczej w przypadku liczb ujemnych, ponieważ zaokrągla się do następnej liczby ujemnej.
Np .: piętro (7.2) to 7.0
piętro (-7, 2) wynosi -8, 0
Przykład:
Ten program ilustruje sposób obliczania dolnego poziomu dla zadeklarowanej wartości i zaokrągla do następnej wartości 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Wynik:

2. ceil ()
Składnia:
double ceil (double b)
Ta funkcja zwraca najmniejszą wartość całkowitą większą lub równą b i zaokrągla wartość w górę. W przypadku wartości ujemnej przesuwa się w lewo. Przykład 3.4 zwraca wartość -3.
Przykład:
Ten program wyjaśnia, przyjmując dane wejściowe w argumencie float i zwraca wartość sufitu.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Wynik:

3. Sqrt ()
Ta funkcja zwraca pierwiastek kwadratowy z określonej liczby.
Składnia:
sqrt( arg)
Przykład:
Poniższy kod wyjaśnia najbardziej znaną funkcję matematyczną sqrt (), biorąc wartości „n” w celu obliczenia pierwiastka kwadratowego dla różnych wartości „n”.
#include
#include
int main()
(
double n, output;
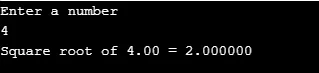
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Wynik:
4. okrągły ()
Ta funkcja zaokrągla najbliższą wartość danego wejścia. Zgłasza błąd, jeśli wartość jest zbyt duża. Inne funkcje, takie jak lround (), llround (), również zaokrąglają najbliższą liczbę całkowitą.
Składnia:
int round(arg)
Przykład:
Poniższy kod jest bardzo prosty, który zaokrągla do najbliższej wartości „r” w pętli for.
#include
#include
int main ()
(
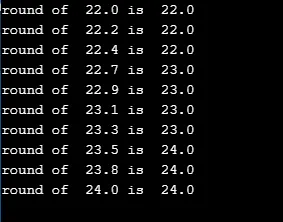
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Wynik:
5.pow ()
Ta funkcja powraca do mocy dla podanej liczby (a b ). Zwraca podniesioną do potęgi b, która ma dwa parametry: podstawę i wykładnik.
Przykład:
W poniższym kodzie źródłowym zezwalamy użytkownikowi na wprowadzenie wartości wejściowej w celu obliczenia mocy podanych dwóch argumentów.
#include
#include
int main()
(
int r, ba, expr;
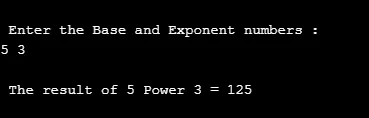
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
wynik:
6. trun ()
Ta funkcja pomaga w skracaniu podanej wartości. Zwraca wartości całkowite. Aby obciąć wartości zmiennoprzecinkowe i podwójne, stosuje się truncf (), truncl ().
Składnia:
double trunc(a);
Przykład:
Poniższy kod źródłowy przyjmuje dwie wartości wejściowe a, b, aby obciąć podwójne wartości.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Wynik:

7. fmod ()
Ta funkcja zwraca resztę dla podanych dwóch wartości wejściowych, gdy m podzielone przez n.
Składnia:
double fmod(double I, double j)
Przykład:
W poniższym przykładzie użytkownik potrzebuje dwóch wartości, aby obliczyć resztę za pomocą funkcji fmod ().
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Wynik:

Funkcje trygonometryczne
Poniżej znajdują się różne funkcje trygonometryczne:
1. sin ()
Ta wbudowana funkcja podaje wartość sinusoidalną podanej liczby, oblicza wartości zmiennoprzecinkowe. asin () oblicza łuk, dla hiperbolicznego jest to sinh ().
Składnia:
return type sin(y);
y zwraca wartość w radianach, a typ zwracany jest podwójnie.
Przykład:
W poniższym kodzie źródłowym wziąłem dwie różne wartości wejściowe, aby obliczyć wartość grzechu i zwraca dwa razy.
#include
#include
int main()
(
double a;
double z;
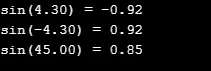
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Wynik:
2. sinh ()
Ta funkcja matematyczna oblicza wartość sinusoidy stycznej trygonometrycznej dla podanej liczby.
Składnia:
double sinh(x);
Przykład
W poniższym kodzie źródłowym sinus hiperboliczny jest obliczany poprzez zadeklarowanie wartości wejściowej.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Wynik

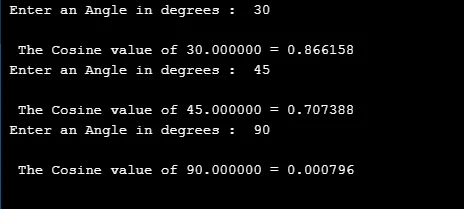
3. cos ()
Ta funkcja matematyczna określa trygonometryczną wartość cosinus dla danego elementu.
Składnia: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Wynik:
4. cosh ()
Zwraca cosinus hyberboliczny dla danej wartości.
Składnia:
double cosh(y);
Przykład
Poniższy przykład pokazuje, że do obliczenia hiperboli potrzeba dwóch różnych wartości wejściowych.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Wynik

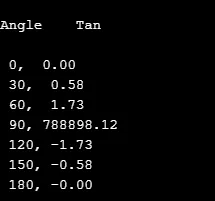
5. tan ()
Ta funkcja biblioteki matematycznej oblicza styczne wartości kąta dla wyrażenia matematycznego i mierzone w radianach.
Można go zadeklarować jako
double tan(arguments);
Przykład
W poniższym kodzie źródłowym wartość tan jest obliczana dla następujących kątów, które są zwiększane za pomocą pętli for.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Wynik:
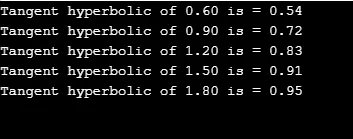
6. tanh ()
Funkcja tanh () zwraca styczną hiperboliczną o podanej wartości. Wymaga jednego parametru. Oprócz znalezienia stycznej dla długich podwójnych i pływających do obliczeń używane są tanhl () i tanhf ().
Składnia:
double tanh( val);
Przykład:
Styczna hyberboliczna jest obliczana dla wartości „j” za pomocą pętli. Zobaczmy, jak to działa.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Wynik:
Rejestruj funkcje arytmetyczne
Poniżej znajdują się różne funkcje arytmetyki dziennika:
1. exp ()
Ta funkcja wykonuje obliczenia wykładnicze dla danej wartości (e x ). Istnieją również inne podtypy, takie jak frexp (), Idexp () zwracające mantysę i pomnożone przez potęgę x.
Składnia:
return type exp(value);
Przykład:
Program pobiera wartość liczbową od użytkownika, aby obliczyć wykładnik dla danej wartości i zwraca dwukrotnie.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Wynik

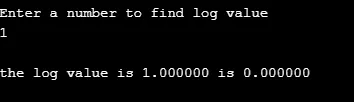
2. log ()
Ta funkcja zwraca wartość logarytmu podanej liczby. (do bazy e. log e )
Składnia:
double log(arg);
Przykład:
W poniższym przykładzie wartość logarytmiczną dla podanej liczby oblicza się za pomocą funkcji. Funkcja zdefiniowana przez użytkownika lgm () wykonuje obliczenia, a funkcja jest wywoływana w funkcji głównej.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
wynik:
Wniosek
Podsumowując, widzieliśmy różne funkcje matematyczne używane w programowaniu w C i są to bezpośrednie funkcje biblioteczne, których należy użyć. Programy C wykorzystują te funkcje do różnych operacji matematycznych. Aby rozwiązać niektóre skomplikowane wersje obliczeń, ta wbudowana funkcja zapewnia matematycznie zorientowany język programowania do zwracania prostych wartości.
Polecane artykuły
Jest to przewodnik po funkcjach matematycznych w C. Tutaj omawiamy różne funkcje matematyczne w C z przykładami. Możesz także przejrzeć nasze inne sugerowane artykuły -
- Funkcje matematyczne PHP
- Funkcje matematyczne JavaScript
- Funkcje przenoszenia w Matlabie
- Funkcje ciągów JavaScript
- Wprowadzenie do funkcji matematycznych w języku Python
- Przegląd funkcji matematycznych w języku C #
- Mnożenie macierzy programowania C.
- Pierwiastek kwadratowy w PHP
- Przykłady pierwiastka kwadratowego w JavaScript